ГЕОДЕЗІЯ

І частина

Електронний посібник

ГОЛОВНА	ТЕОРЕТИЧНІ ВІДОМОСТІ	АНОТАЦІЯ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ			УКЛАДАЧІ

8. ПЛОСКІ ПРЯМОКУТНІ КООРДИНАТИ ГАУСА

8.1. Загальні поняття про картографічні проєкції

8.1.1. Класифікація картографічних проєкцій

8.1.2. Система географічних координат

8.1.3. Рівнокутна поперечно-циліндрична проєкція Гауса

8.2. Плоскі прямокутні координати Гауса

8.2.1. Суть та принципи побудови системи Гауса. Шестиградусні та триградусні зони

8.2.2. Спотворення довжин ліній і площ у проєкції Гауса

8.2.3. Перекриття зон

8.3. Розграфлення та номенклатура листів топографічних карт і планів

8.3.1. Визначення номенклатури листів карт масштабу 1:1 000 000

8.3.2. Визначення номенклатури листів карт масштабу 1:500 000, 1:300 000, 1:200 000,

1:100 000

8.1. Загальні поняття про картографічні проєкції

8.1.1. Класифікація картографічних проєкцій

Земля та і будь-яке інше небесне тіло має надзвичайно складну форму поверхні. На ній і практично неможливо визначати положення об'єктів, відстані між ними або напрямки, якщо ці об'єкти розташовані на значних відстанях. Тому в геодезії та картографії для вирішення практичних завдань Землю описують за допомогою спрощених математичних моделей. Реальна поверхня Землі заміняється на математичну поверхню Землі, будь-яка точка якої має чітке визначення через певний набір рівнянь.

За математичну поверхню Землі приймається поверхня еліпсоїда обертання з полярним стисненням або поверхня кулі, якщо умови задачі дозволяють нехтувати значенням полярного стиснення. Математичну поверхню Землі можна визначити за результатами геодезичних, астрономічних, гравіметричних вимірювань; вона однозначно описується рівнянням еліпсоїда (кулі).

Але навіть за такого спрощення передавати на паперових картах зображення значних за розмірами ділянок земної поверхні неможливо без вирішення ще однієї задачі – перетворення зображення на поверхні еліпсоїда у зображення в картографічній проєкції.

Картографічні проєкції – це спосіб зображення на площині математичної поверхні Землі. Картографічна проєкція задається математичним законом, що встановлює однозначний зв'язок між координатами математичної поверхні Землі і відповідними плоскими координатами цих же точок у зображенні.

Цей математичний закон записується у вигляді рівнянь картографічної проєкції.

У загальному випадку рівняння картографічних проєкцій мають вигляд:

,

де: φ і λ – географічні координати точки на математичній поверхні Землі;

х і у – прямокутні координати зображення цієї точки в площині в проєкції.

Зрозуміло, що від властивостей і характеру функцій f₁ і f₂ будуть залежати і властивості проєкції.

Існує низка вимог до функцій картографічних проєкцій:

- функції f₁ і f₂ мають бути однозначними;

- частинні похідні функцій мають бути безперервними;

- детермінант системи рівннянь має бути більшим за нуль.

Оскільки таких функцій можна визначити безліч, то і проєкції можуть бути дуже різноманітними.

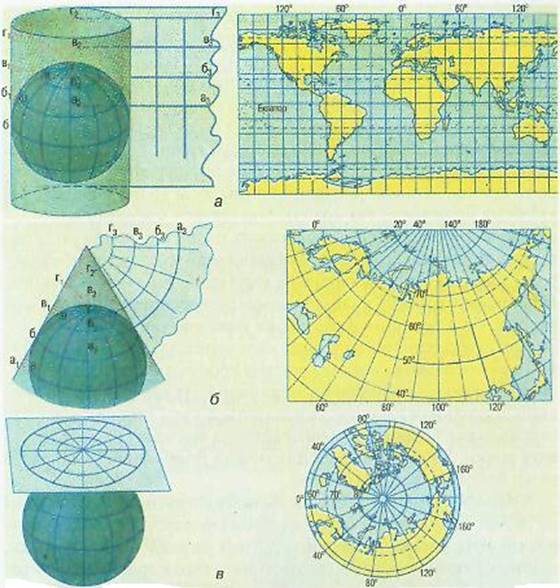
Зобразити поверхню еліпсоїду або кулі в площину можна за законами проєктивної геометрії.

Для створення карт використовують певні допоміжні геометричні фігури. За видом допоміжної поверхні картографічні проєкції поділяються на циліндричні, азимутальні та конічні.

Рис. 87. Картографічні проєкції за видом допоміжної площини:

а) циліндрична; б) конічна; в) азимутальна

Азимутальними називають такі картографічні проєкції, коли поверхня Землі (а точніше її градусна сітка) проєктується з певної точки, на площину. Якщо допоміжна площина дотична до полюса, то така проєкція називається нормальною, а якщо до екватора – поперечною. Перші використовують для зображення територій у приполярних широтах. Характерною ознакою їхньої градусної сітки є меридіани у вигляді прямих ліній, що виходять із однієї точки, і паралелі – концентричні кола. В азимутальних поперечних проєкціях зображуються карти півкуль та територій у приекваторіальних широтах. Прямою лінією на карті є тільки екватор.

Створюючи географічну карту за допомогою циліндричної проєкції, земну поверхню переносять на бічну проєкцію уявного циліндра. Його вісь може збігатися з віссю Землі, тоді проєкція називається нормальною, а може бути перпендикулярною до неї – поперечною. Перша з них використовується для карт світу, материків і країн, що розміщені у низьких (близьких до екватора) широтах. Характерною ознакою їх є те, що паралелі і меридіани є прямими лініями. Поперечна циліндрична проєкція використовується для створення топографічних карт.

У конічних проєкціях як допоміжна фігура використовується конус, вісь якого збігається з віссю Землі. Конічні проєкції використовують для зображення материків і країн, які розміщені у середніх широтах. Градусну сітку таких карт утворюють меридіани у вигляді прямих ліній, що виходять з однієї точки, та паралелі, що є дугами концентричних кіл.

Щоб створити карту світу, використовують декілька допоміжних конусів і таку проєкцію називають поліконічною. Отримані фрагменти картографічної сітки, що відображають різні широтні смуги, з'єднують між собою. Тому меридіани – криві лінії, а паралелі – дуги неконцентричних кіл.

Порушення геометричних розмірів і форм ділянок земної поверхні, розміщених на них об'єктів під час їхнього зображення на площині називають картографічними спотвореннями. Розрізняють чотири види спотворень: довжин ліній, кутів, форм та площ.

Наявність спотворення відстаней вздовж паралелей дізнаються за довжинами відрізків екватора і паралелі 60^º широти між сусідніми меридіанами. Відрізок екватора має бути рівно удвічі більший, ніж відрізок паралелі 60^º широти. Якщо це співвідношення інше, то на карті існують спотворення довжин ліній за напрямком паралелей.

Про спотворення відстаней по паралелі свідчать співвідношення довжин відрізків екватора і паралелі 60^º широти між сусідніми меридіанами. Коли спотворення відсутні, то відрізок екватора удвічі більший, ніж відрізок паралелі 60^º широти.

Спотворення кутів є характерним для більшості карт, можна зробити висновок у тому випадку, коли паралелі й меридіани не утворюють між собою прямих кутів.

Розрізнити спотворення форм можна, порівнявши довжину й ширину будь-якого географічного об'єкта на карті та глобусі. Якщо співвідношення в обох випадках рівні, то спотворень форм немає. Ще простіше це зробити, якщо порівняти клітинки сітки на одній широті: коли вони однакові, то спотворення форм на цій географічній карті відсутні.

Якщо площі двох клітинок між сусідніми паралелями рівні, то на цій географічній карті немає спотворення площ.

За характером спотворень картографічні проєкції поділяють на рівновеликі (немає спотворень площ), рівнокутні (немає спотворень кутів) і довільні (усі види спотворень зводяться до мінімуму). Серед останньої групи карт виділяють підгрупу рівнопроміжних, коли відсутні спотворення довжин ліній за одним із напрямків (уздовж меридіанів або вздовж паралелей). Отже, відстані на картах можуть бути неспотворені тільки за одним із напрямків, але на більшості карт вони не відповідають єдиному масштабу в усіх напрямках. Масштаб, що вказаний на карті, є середнім, а тому він непридатний для визначення відстаней на дрібномасштабних картах.

8.1.2. Система географічних координат

Положення точки на фізичній поверхні Землі визначається системою координат – лінійними та кутовими величинами. В геодезії використовують різні системи координат. Складаючи карти великих територій земної поверхні та працюючи на них, користуються географічними координатами. Ними є кутові величини (довгота й широта), які визначають положення точки на поверхні еліпсоїда відносно екватора і початкового меридіана.

Рис. 88. Географічні координати точки

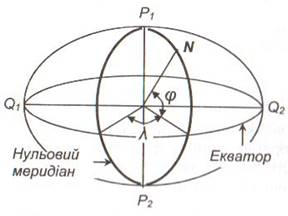
Географічні координати можуть бути геодезичними і астрономічними. Останні задаються як довгота і широта, значення яких отримують із астрономічних спостережень.

Географічна широта φ – кут між прямовисною лінією в даній точці і площиною екватора. Відлічується по обидва боки від екватора і змінюється від 0^º до 90^º. Розрізняють північну та південну широти.

Географічна довгота λ – двогранний кут між площинами початкового меридіана та меридіана даної точки. Відлічується по обидва боки від початкового меридіана і змінюється від 0^º до 180^º. У східній півкулі довготи східні, у західній – західні.

8.1.3. Рівнокутна поперечно-циліндрична проєкція Гауса

Щоб зобразити на площині сферичну поверхню Землі у вигляді карти, на площину переносять мережу меридіанів і паралелей – картографічну сітку – і потім за географічними координатами точок земної поверхні будують карту. У геодезії доцільно застосовувати таку проєкцію, що не спотворювала б кутів, тобто зберігала б подобу зображуваних фігур. Такі проєкції називають рівнокутними (конформні).

Рис. 89. Зональна система координат Гаусса-Крюгера

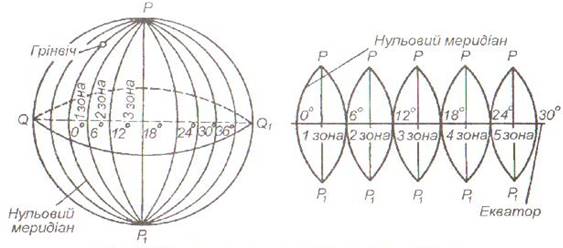
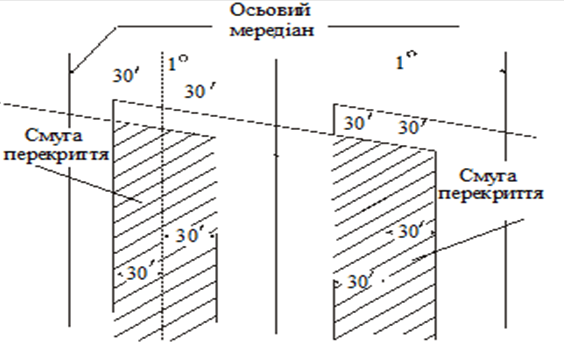
Теорію конформного зображення однієї поверхні на іншу і, зокрема зображення поверхні земного еліпсоїда на площині було розроблено німецьким вченим К.Ф.Крюгером у 1825 – 1830 рр., але практичне розповсюдження вона дістала після виведення Л.Крюгером у 1912 р. робочих формул, зручних для обчислень у цій проєкції. При використанні проєкції Гауса-Крюгера поверхня еліпсоїда поділяється меридіанними площинами на зони.

	ПРЕЗЕНТАЦІЯ
	Питання для самоперевірки
1. Що прийнято за математичну поверхню Землі? 2. Що таке картографічна проєкція? 3. Суть азимутальної картографічної проєкції. 4. Суть конічної картографічної проєкції. 5. Суть циліндричної картографічної проекції. 6. Що таке картографічне спотворення? 7. Які види спотворень? 8. Які існують картографічні проєкції за характером спотворень? 9. Що таке система координат? 10. Що таке географічні координати? 11. Які проєкції називають рівнокутними? 12. Як визначити географічні координати точки на топографічній карті?

8.2. Плоскі прямокутні координати Гауса

8.2.1. Суть та принципи побудови системи Гауса. Шестиградусні та триградусні зони

Проєкцію Гауса–Крюгера одержують, проєктуючи земну кулю на поверхню циліндра, що торкається Землі, по будь-якому меридіану. Щоб перекручування довжини ліній не перевищували меж точності масштабу карти, проєкційну частину земної поверхні обмежують меридіанами з різницею довгот 6^°, а під час складання планів у масштабах 1:5 000 і крупніше – 3^°. Така ділянка називається зоною. Середній меридіан у кожній зоні називається осьовим. Рахунок зон ведеться від Гринвіцького меридіана на схід.

Поперечно-циліндрична проєкція

Гауса-Крюгера 6-та зона, початок від

Рис. 90. Шести градусна зона

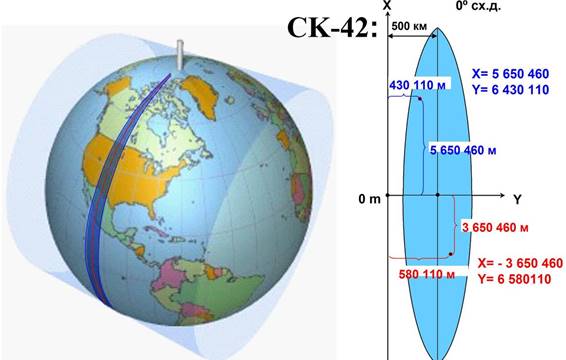
Після розгортання циліндра в площину осьовий меридіан зони й екватор зобразяться взаємно перпендикулярними прямими лініями (проєкція осьового меридіана) і (проєкція екватора).

Зображення осьового меридіана й екватора приймають за осі зональної системи прямокутних координат з початком у точці їхнього перетинання. Із зображенням осьового меридіана сполучають вісь абсцис X, а екватора – вісь ординат У.

Для всіх точок на території нашої країни абсциси мають позитивне значення. Для того щоб ординати точок також були тільки позитивними, у кожній зоні ординату початку координат приймають рівною 500 км. Таким чином, точки, розташовані на захід від осьового меридіана, мають ординати менше 500 км, а до сходу – понад 500 км. Ці ординати називають перетвореними.

Для зручності користування плоскими прямокутними координатами на кожен аркуш топографічної карти, починаючи з масштабу 1:200 000, наносять сітку квадратів, що називається кілометровою сіткою. Сторони квадратів паралельні осям Х и У даної зональної системи координат. Розміри сторін залежать від масштабу карти. Наприклад, на картах масштабів 1:10 000 –
1:50 000 сторони квадратів відповідають 1 км на місцевості.

Так як осьові меридіани зон не паралельні одна одній, кілометрові сітки двох суміжних зон не збігаються, тому на картах, розташованих у межах 2^° по довготі уздовж західної й східної меж зони, показують виходи координат сітки сусідніх зон.

8.2.2. Спотворення довжин ліній і площ у проєкції Гауса

По мірі віддалення точок від осьового меридіана зони ростуть спотворення довжин ліній, досягаючи максимальної величини на межі координатної зони. Їх величина Δs визначається за формулою

де: S – довжина на площині проєкції;

s – довжина відповідної лінії на еліпсоїді;

y – середня ордината лінії;

R – середній радіус земної кулі (R=6371 км)

Масштаб у напрямку меридіана=1. Чим дальше від меридіана до межі зони, тим спотворення більше.

Масштаб спотворень m у інших місцях зони можна визначити за формулою:

За максимального значення y_max=334 км відносне спотворення довжин ліній під час проєктування на площину складає 1:745. Для нашої країни, розташованої північніше паралелі з широтою 44° максимальна ордината дорівнює орієнтовно 236 км, а максимальне спотворення ліній на краю 6-градусної зони складає близько 1:1 100.

Ці спотворення знаходяться в межах помилки графічних побудов для масштабів 1:10 000 і дрібніше.

У 3-градусній зоні максимальні спотворення в 4 рази менші, ніж у 6-градусній зоні. Тому під час зйомок у масштабах 1:5 000 й крупніше координати обчислюються в 3-градусних зонах.

Аналіз точності визначення площ ділянок поверхні еліпсоїда за плоскими прямокутними координатами їхніх вершин у проєкції Гауса показує, що в межах однієї координатної зони площу будь-якої земельної ділянки можна обчислити з похибкою до 1 квадратного метра. Для значних територій, які розташовані в декількох координатних зонах, похибка визначення площі не перевищує 5 – 10 квадратних метрів або 10^-10 – 10^-12 % від площі ділянки.

8.2.3. Перекриття зон

Рис. 91. Схема перекриття зон

У практиці геодезичних робіт потреба перетворювання плоских координат X_I, Y_I в координати X_II, Y_II, тобто необхідність перейти від однієї системи плоских прямокутних координат до другої, зустрічається доволі часто.

Наприклад, математичне опрацювання геодезичної мережі в системі плоских прямокутних координат Гауса-Крюгера, пункти якої розміщені по обидва боки від граничного меридіана сусідніх смуг на еліпсоїді, можливе тоді, якщо координати вихідних пунктів для цієї мережі будуть в одній системі плоских координат, тобто в одній координатній зоні.

Під час розв'язування оберненої геодезичної мережі на площині між пунктами, розміщеними в різних смугах на еліпсоїді плоскі координати мають бути задані в одній координатній зоні.

Для таких і їм подібних випадків, що нерідко зустрічаються на практиці, передбачено під час створення каталогів плоских прямокутних координат "перекриття” зон. Всі пункти, розміщені на 30´ по довготі на схід і захід від граничного меридіана шестиградусних смуг у каталогах мають координати в двох зонах: відносно осьового меридіана L_o=const своєї зони і осьового меридіана L_o+l_o=const сусідньої зони. Схематично таке перекриття зображено на рис.91. Цим, фактично, протяжність шестиградусних зон по довготі збільшується до 7° та створюється перекриття в 1°.

	ПРЕЗЕНТАЦІЯ
	Питання для самоперевірки
1. Як одержують проєкцію Гауса-Крюгера? 2. Яка ділянка називається зоною? 3. Які ординати називають перетвореними? 4. Коли застосовується перекриття зон? 5. Який меридіан називається осьовим? 6. Як спотворюються довжини ліній та площ у проєкції Гауса?

8.3. Розграфлення та номенклатура листів топографічних карт і планів

8.3.1. Визначення номенклатури листів карт масштабу 1:1 000 000

Для визначення положення окремих аркушів карт на поверхні земної кулі розроблено систему їх обліку та позначення.

Номенклатура – це система позначення окремих листів карт. Верхньою (північною) та нижньою (південною) сторонами рамки служать паралелі, а боковими (західною та східною) – меридіани. Номенклатура кожного аркуша карти масштабу 1:1 000 000 складається з позначення пояса і номера колони.

Враховуючи, що найменший масштаб топографічної карти є 1:1 000 000, для відображення на топографічній карті всієї земної поверхні, або лише її частини, наприклад, рівної за розмірами території України, потрібно буде створити карту дуже великих розмірів. Однак такою картою було б важко користуватися на практиці. Тому зображення земної поверхні для відтворення на топографічних картах з давніх часів прийнято поділяти на окремі фрагменти-аркуші. Система такого поділу карти на окремі аркуші називається розграфкою карти.

Рис. 92. Розграфлення карт

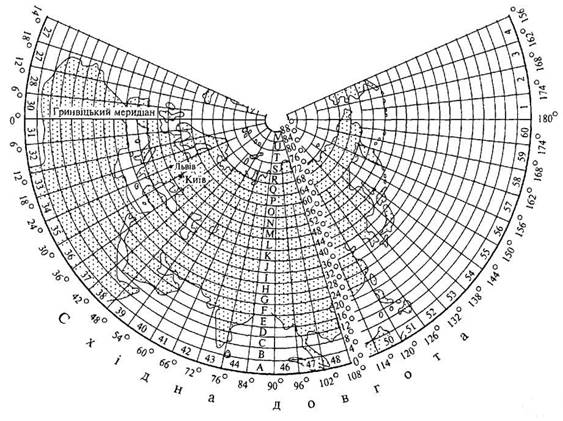
Основою розграфлення та номенклатур аркушів топографічних карт масштабів 1:10 000 – 1:500 000 є міжнародне розграфлення та номенклатури аркушів карти масштабу 1:1 000 000. Аркуші цієї карти по паралелях створюють пояси, кожен по 4° широти, а по меридіанах – колони, кожна по 6° довготи. Пояси позначаються великими літерами латинського алфавіту (від А до V), починаючи від екватора на північ та на південь, а колони – арабськими цифрами (від 1 до 60) від меридіана 180° з заходу на схід. 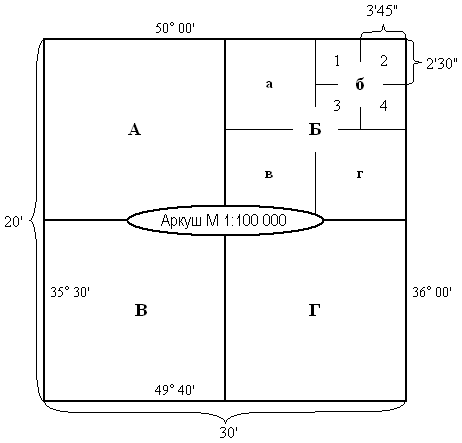Номенклатура, аркуша карти 1:1 000 000 складається з номеру поясу та колони, наприклад, M-37, L-35 тощо.

8.3.2. Визначення номенклатури листів карт масштабу 1:500 000, 1:300 000, 1:200 000, 1:100 000

Аркуші карти масштабу 1:500 000 отримуються поділом карти масштабу 1:1 000 000 на 4 аркуші з розмірами 2° по широті та 3° по довготі (рис. 93 а), які позначаються великими літерами А, Б, В, Г. Номенклатура аркуша карти масштабу 1:500 000 включає позначення аркуша карти 1:1 000 000 та відповідну літеру А, Б, В або Г, наприклад, M-37-А, L-35-В.

Рис. 93 а. Схема розграфки аркушу карти 1:1 000 000 на аркуші карти масштабу 1:500 000	Рис. 93 б. Схема розграфки аркушу карти 1:1 000 000 на аркуші карти масштабу 1:200 000

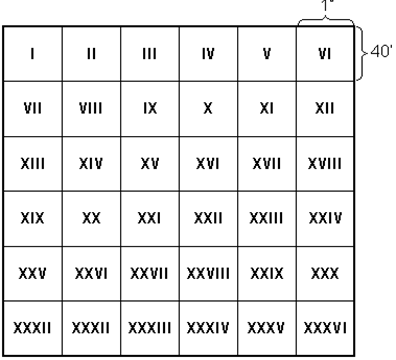
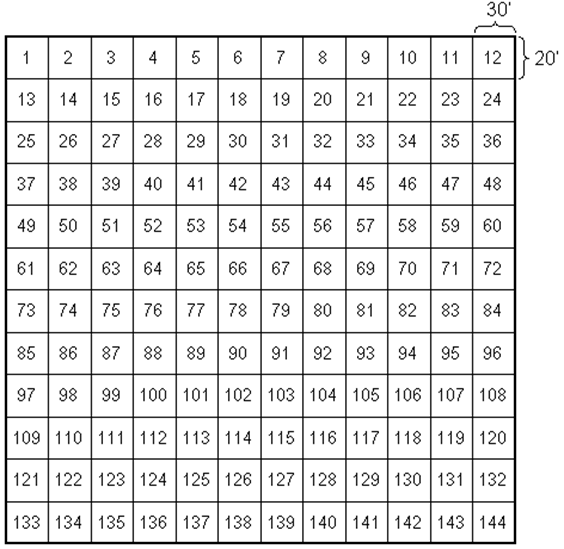
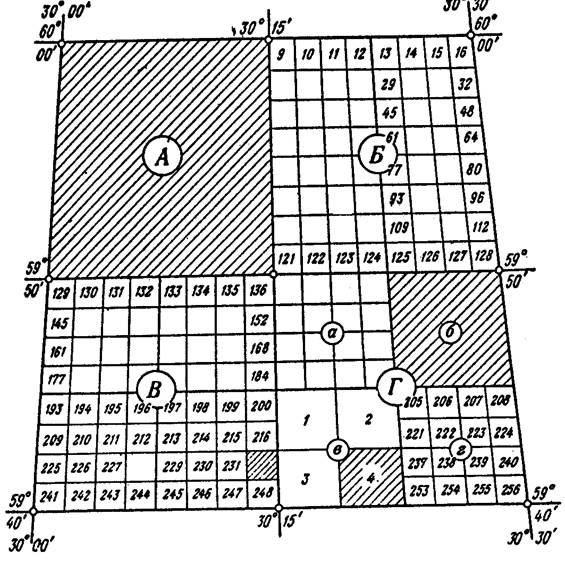
Аркуші карти масштабу 1:200 000 отримуються поділом карти масштабу 1:1 000 000 на 36 аркушів з розмірами 40' по широті та 1 по довготі (рис. 93 б), які позначаються римськими цифрами від I до XXXVI. Номенклатура аркуша карти масштабу 1:200 000 складається з номенклатури аркуша карти
1:1 000 000 та відповідної римської цифри, наприклад, M-37-I або L-35-XXV.

Аркуші карти масштабу 1:100 000 отримується поділом карти масштабу 1:1 000 000 на 144 аркуші з розмірами 20' по широті та 30' по довготі (рис. 94), які позначаються арабськими цифрами від 1 до 144. Номенклатура аркуша карти масштабу 1:100 000 складається з номенклатури аркуша карти
1:1 000 000 та відповідної арабської цифри, наприклад, M-37-142 або L-35-12.

Рис. 94.

Схема розграфки аркушу карти 1:1 000 000 на аркуші карти масштабу 1:100 000

Аркуш карти масштабу 1:100 000 є основою розграфлення топографічних карт масштабів 1:10 000 – 1:50 000 (рис. 95). Аркуш карти масштабу 1:100 000 містить 4 аркуші карти масштабу 1:50 000, які позначаються великими літерами – А, Б, В, Г. Аркуш карти масштабу 1:50 000 містить 4 аркуші карти масштабу 1:25 000, які позначаються малими літерами – а, б, в, г. Аркуш карти масштабу 1:25 000 містить 4 аркуші карти масштабу 1:10 000, які позначаються арабськими цифрами – 1, 2, 3, 4.

Рис. 95. Схема розграфлення аркушу карти 1:100 000

на акуші карт М 1:50 000, 1:25 000, 1:10 000

Таблиця 11

Номенклатури та розміри рамок карт різних масштабів

Масштаб карти	Приклад номенклатури	Розміри аркуша
		по широті	по довготі
1:1 000 000	M-36	4°	6°
1:500 000	M-36-А	2°	3°
1:200 000	M-36-XXI	40'	1°
1:100 000	M-36-132	20'	30'
1:50 000	M-36-132-А	10'	15'
1:25 000	M-36-132-А-б	5'	7'30''
1:10 000	M-36-132-А-б-4	2'30''	3'45''

Одному аркушу карти масштабу 1:100 000 відповідають 256 аркушів карт масштабу 1:5 000, які позначають арабськими цифрами від 1 до 256. Номенклатура аркуша карти масштабу 1:5 000 складається з номенклатури аркуша карти масштабу 1:100 000 з додаванням у дужках порядкового номера аркуша карти масштабу 1:5 000, наприклад, О-36-I-(232) (Рис. 96).

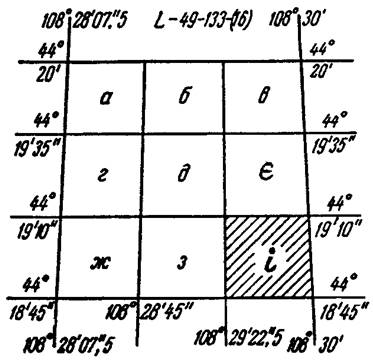
Одному аркушу карти масштабу 1:5 000 відповідають 9 аркушів карти масштабу 1:2 000, що позначаються малими літерами українського алфавіту а, б, у, м, д, є, ж, з, і. Номенклатура кожного аркуша карти масштабу 1:2 000 складається з номенклатури карти масштабу 1:5 000 з додаванням у дужках відповідної букви , наприклад, L-49-133-(16-і) (рис. 97).

Рис. 96. Розграфлення і позначення аркушів карт масштабів

1:50 000, 1:25 000, 1:10 000 і 1:5 000

В основу квадратного розграфлення приймають аркуш масштабу 1:5 000, що позначається арабською цифрою. Порядок нумерації аркушів плану масштабу 1 5 000 встановлює установа, яка видає дозвіл на проведення топографо-геодезичних робіт.

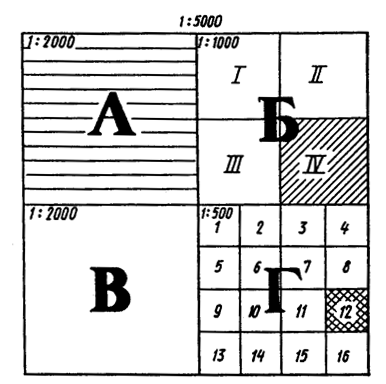
Одному аркушу плану масштабу 1:5 000 відповідають чотири аркуші плану масштабу 1: 2000, які позначаються великими літерами українського алфавіту А, Б, В і Г, які записують після арабської цифри аркуша плану масштабу 1:5000, наприклад, 4-А (Рис. 96).

Одному аркушу плану масштабу 1: 2 000 відповідають чотири аркуші плану масштабу 1: 1 000, що позначаються римськими цифрами I, II, III і IV і 16 аркушів плану масштабу 1: 500, що позначаються арабськими цифрами 1, 2, 3...16 (Рис. 96).

Рис. 97. Розграфлення і позначення аркушів планів масштабів 1:2 000, 1:1 000 і 1:500

Номенклатура аркушів планів масштабу 1:1 000 і 1:500 складається з номенклатури аркуша плану масштабу 1:2 000 і відповідної римської цифри для масштабу 1:1 000 або арабської цифри для аркуша плану масштабу 1:500, наприклад 4-Б-IV (1:1 000) і 4-Г-12 (1:500) (рис. 97).

browser does not support the video tag.
	https://www.youtube.com/watch?v=2Gv9dSEJsz8&t=11s

	ПРЕЗЕНТАЦІЯ
	Питання для самоперевірки
1. Що таке номенклатура топографічних карт та планів? 2. Що таке розграфлення топографічних карт та планів? 3. Які основні принципи покладені в основу розграфлення і номенклатури топографічних карт в Україні? 4. З чого складається номенклатура аркуша карти масштабу 1: 1000000? 5. Які розміри рамок топографічних карт масштабів 1: 500000, 1: 200000, 1: 100000?

Попередня тема

На початок

Наступна тема