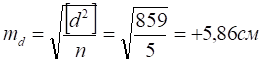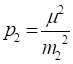НМЦ

ГЕОДЕЗІЯ

І частина

Електронний посібник

 

ВФПО

 

7.1. Рівноточні вимірювання

7.1.1. Загальні відомості про похибки вимірювань, види та їх властивості

7.1.2. Середня квадратична похибка окремого вимірювання та середнього арифметичного

7.1.3. Визначення середньої квадратичної похибки одного виміру із ряду рівноточних вимірювань

7.1.4. Обробка ряду рівноточних вимірів з оцінкою точності вимірювань

7.2. Нерівноточні вимірювання

7.2.1. Нерівноточні вимірювання, їх вага. Середня квадратична похибка одиниці ваги

7.2.2. Середня квадратична похибка вагового середнього

 

 

Вимірювання ліній і кутів на місцевості та на планах (картах) проводиться не абсолютно точно. Це пояснюється неточністю приладів, недосконалістю ока людини, нерівністю місцевості, недоліками освітлення, змінами температури та вологості повітря тощо. Для підвищення точності вимірювань одну й ту ж величину (лінію або кут) вимірюють кілька разів із одержаних результатів l1, l2,  l3... виводять середнє (найімовірніше) значення L. Його називають арифметичною серединою.

 

 

Однак і такий результат вимірювання не можна вважати абсолютно точним, оскільки він теж містить похибку.

Похибкою вимірювання Δ (дельта) називають різницю між результатом вимірювання L і точним значенням вимірюваної величини а, тобто

 

Δ = L – а.

 

Таку похибку називають абсолютною.

Похибки вимірювань можуть бути великими й малими, додатними й від'ємними, але за певних умов вони за абсолютною величиною не можуть перевищувати якусь межу. Така похибка називається гранично-допустимою.

Довірою до результатів вимірювань є оцінка його точності. Похибки поділяють на: грубі, систематичні та випадкові.

Грубі похибки – прорахунки у вимірюваннях, які суттєво перевищують у даних умовах очікувані похибки.

Систематичні похибки – виникають від постійного джерела, мають визначений знак і величину.

Випадковими похибками – називаються такі похибки, які за повторних вимірювань однієї і тієї ж величини можуть набувати тих або інших значень.

 

 

Крім граничнодопустимих похибок, точність вимірювань характеризують середні та середньоквадратичні похибки (СКП), які вираховують за формулою:

 

,

 

де: Δ = L – а – відхилення від середнього значення;

n – кількість вимірювань.

Для оцінки точності середнього значення вимірюваної величини використовують відому формулу:

 

,

 

де: М – СКП середнього значення вимірюваної величини.

Крім величини m і M на практиці часто користуються відносними похибками, для обчислення відносної похибки необхідно взяти відношення абсолютної похибки до деякого значення вимірюваної величини або, відповідно, її середнього значення.

 

7.1.3. Визначення середньої квадратичної похибки одного виміру із ряду рівноточних вимірювань

 

Результати обробки вимірювань віддалі між двома точками.

Знайти:

• СКП одного вимірювання;

• середнього значення;

• відносну похибку.

 

Таблиця 6

№ з/п

Результати вимірів, м

Δ

Δ ²

Обчислення

1

165,25

-0,01

0,0001

 

Похибки:

а) середня квадратична одного вимірювання:

 

б) середнього значення:

 

в) відносна

2

165,15

+0,09

0,0081

3

165,12

+0,12

0,0144

4

165,18

+0,06

0,0036

5

165,29

-0,05

0,0025

6

165,31

-0,07

0,0049

7

165,36

-0,12

0,0144

8

165,18

+0,06

0,0036

9

165,27

-0,03

0,0009

10

165,30

-0,06

0,0036

 

L = 165.24

-0.01

0.0561

 

Вимірювання, які мають однакові середні квадратичні похибки називаються рівноточними.

 

7.1.4. Обробка ряду рівноточних вимірів з оцінкою точності вимірювань

 

Задача 1. Вирахувати СКП одного вимірювання. Кут виміряний 9 разів. Істинна величина кута

L =152º18’40”, СКП одного виміру

 

 

 

Допустима помилка 3m= ± 10,24”.

 

Таблиця 7

Вимірювання

Результати вимірів

Δ = L-а

Δ 2

1

152º18’46”

-6

36

2

152º18’37”

+3

9

3

152º18’24”

+16

256

4

152º18’41”

-1

1

5

152º18’52”

-12

144

6

152º18’27”

+13

169

7

152º18’36”

+4

16

8

152º18’52”

-12

144

9

152º18’27”

+13

169

 

Істинне значення

L = 152º18’40’’

-37

+49

944

 

Задача 2. Лінія між точками виміряна стрічкою 5 разів.

 

Таблиця 8

Вимірювання

Результати вимірів

Відхилення від наймовірнішого значення Δ

Квадрати відхилень Δ2

1

356.21

+0.29

0.0841

2

356.74

-0.24

0.0576

3

356.37

+0.13

0.0169

4

356.48

+0.02

0.0004

5

356.70

-0.20

0.0400

n=5

L = 356.50

[Δ] = 0

[Δ 2] = 0.1994

 

1. Середня арифметична довжина лінії L = 356,50 м

2. Cередня квадратична похибка окремого вимірювання

 

 

3. Середня квадратична похибка арифметичної середини

 

 

4. Допустима похибка

 

Δдоп =3m= ± 0,12 м.

 

Задача 3. Знайти СКП одного виміру ліній за різницями двох рівноточних вимірів.

 

Таблиця 9

№

вимірів

Вимірювання

d, см

d2

перше

друге

1

152,65

152,84

- 19

361

2

371,22

371,05

+ 17

289

3

527,84

527,90

- 6

36

4

115,37

115,24

+ 13

169

5

141,14

141,16

- 2

4

 

 

 

[d]= +3

[d2] = 859

 

             m = ± 5.86см            

 

 

7.2. Нерівноточні вимірювання

7.2.1. Нерівноточні вимірювання, їх вага. Середня квадратична похибка одиниці ваги

 

У практиці геодезичних вимірювань мають місце випадки, коли одна і та ж величина вимірюється декілька разів нерівноточно, тобто вимірювання мають різні середні квадратні похибки.

За спеціальну міру відносної точності вимірювань прийнята величина, яка називається вагою.

Вага – це спеціальна характеристика відносної точності результатів вимірювань та їх функції, що обчислюється як величина, зворотньо пропорційна до квадратів середніх квадратичних похибок (вага – ступінь надійності).

Нехай вимірювання l1,l2…ln мають відповідно СКП m1, m2…mn.

Тоді ваги p1,p2…pn, що характеризують їх відносну точність, визначаються відношенням:

 

                    

 

де: μ – загальний коефіцієнт пропорційності, або це СКП вимірювань, вага якого = 1 (p=1).

 

 

За нерівноточних вимірювань за найкраще наближення до шуканої величини L приймають загальну арифметичну середину Х, що обчислюється за формулою:

 

,

 

яку часто називають середньоваговим.

Задача 1. Під час вимірювання двох ліній мірною стрічкою були отримані 312,60 і 142,84 м, точне значення яких дорівнює 312,70 м і 142,80 м. Яка з ліній виміряна точніше?

312,70 – 312,60 = 0,10 м

142,84 – 142,80 = 0,04 м

 

                      

 

Нерівноточні вимірювання

 

Задача 2. Дано результати виміру одного кута теодолітами різної точності. Знайти остаточне значення кута. Коефіцієнт с = 50.

 

Таблиця 10

№ з/п

Виміряні

кути

СКП

кута т

ℓ– L0 = έ

έ∙p

Марка теодоліта

1

231º41'25"

5"

15

2

30

ТТ-3

2

231º41'15"

10"

5

0,5

2,5

ТТ-5

3

231º41'14"

20"

4

0,125

0,5

ТМ

4

231 41'36"

15"

26

0,22

5,7

ОТМ

 

L0 = 231º41'10"

 

 

[p] = 2,845

[έ p]=38,7

 

 

L0 – приближенне значення кута

 

 

Попередня тема

На початок

Наступна тема