ГЕОДЕЗІЯ

І частина

Електронний посібник

ГОЛОВНА	ТЕОРЕТИЧНІ ВІДОМОСТІ	АНОТАЦІЯ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ			УКЛАДАЧІ

3. ОБРОБКА МАТЕРІАЛІВ ТЕОДОЛІТНОГО ЗНІМАННЯ

3.1. Обробка матеріалів теодолітної зйомки та складання плану

3.1.1. Плоскі прямокутні координати

3.1.2. Пряма та обернена геодезичні задачі

3.1.3. Послідовність камеральної обробки матеріалів теодолітної зйомки

3.1.4. Обробка кутових вимірювань у теодолітних ходах

3.1.5. Визначення дирекційних кутів та румбів сторін теодолітного ходу

3.1.6. Обчислення та урівнювання приростків координат

3.1.7. Обчислення координат точок теодолітних ходів

3.1.8. Складання плану теодолітної зйомки

3.1. Обробка матеріалів теодолітної зйомки та складання плану

3.1.1. Плоскі прямокутні координати

Положення точки на фізичній поверхні Землі визначається системою координат – лінійними та кутовими величинами. У геодезії використовують різні системи координат.

	Складаючи плани невеликих ділянок землі, користуються місцевою системою прямокутних координат, початком якої може бути будь-яка точка земної поверхні, а положення точки на площині визначається шляхом її проєктування на дві взаємно перпендикулярні прямі – вісь ординат і вісь абсцис.
Рис. 40. Система прямокутних координат

Проводячи геодезичні знімання,часто користуються полярними координатами. За їх початок (полюс) приймають точку, координати якої відомі, а за початковий напрям – напрям на іншу точку з відомими координатами. Положення точки А на місцевості визначають за кутом Ө між початковим напрямом та напрямом на дану точку і відстанню d до неї.
	Рис. 41. Система полярних координат

3.1.2. Пряма та обернена геодезичні задачі

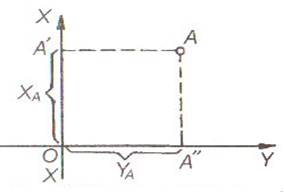
У геодезії прийнято систему плоских прямокутних координат, в якій відносно осі ХХ, що збігається з напрямом меридіана, і осі УУ, перпендикулярній до осі ХХ, визначають положення кожної точки, тобто її координати х і у; при цьому чверті лічать за ходом стрілки годинника, відповідно до зростання азимутів і дирекційних кутів.

Складаючи плани, ситуацію накладають від опорних точок і ліній, що їх сполучають. Тому на папір спочатку наносять опорні точки за їх координатами.

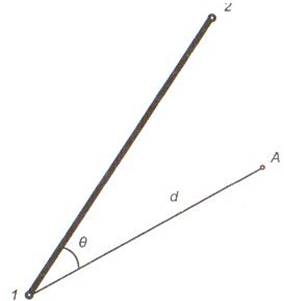
Пряма і зворотна задачі є головними геодезичними задачами. На їх основі базуються всі геодезичні побудови та обчислення.

Пряма геодезична задача полягає в тому, що за відомими координатами х_а, у_а точки А, горизонтальному прокладанню d_АВ лінії АВ, дирекційному куті цієї лінії а_АВ, необхідно визначити координати точки В.

Рис. 42. Пряма та обернена геодезична задача

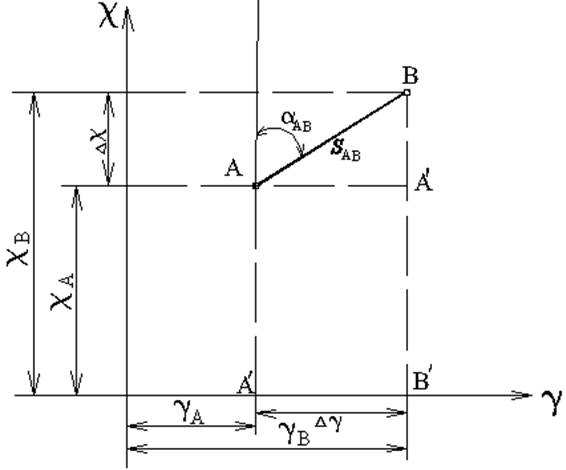
Проведемо з точок А і В лінії паралельні осям координат, відрізки Х_АХ_В та У_АУ_В, що являють собою проекції лінії АВ на осі координат точок А і В, називають приростами координат і позначають ∆ х і ∆у. Тому можна написати:

х_В = х_А + ∆ х;

у_В = у_А + ∆ у.

∆ х і ∆ у можна визначити з прямокутного трикутника АВВ₁

∆ х = d cos a;

∆ y = d sin a. (1)

Тоді координати точки В будуть

х_В = х_А + d cos a;

у_В = у_А + d sin a. (2)

тобто координата точки наступної дорівнює координаті даної точки плюс відповідний приріст між цими точками.

Формули (1) дають розв’язок прямої геодезичної задачі.

Формули (2) залишаються правильними для обчислення приростів координат за румбами сторін, тобто

∆ х = d cos r;

∆ y = d sin r.

Знаки приростів залежать тільки від напряму лінії, тобто величини дирекційного кута або назви румба, наведено в табл.1.

Таблиця 1

Знаки приростів координат

Дирекційні кути	Назва румба лінії	В яку чверть напрямлена лінія	Знаки приростів координат
			∆ х	∆ у
0º – 90º	Пн С	І	+	+
90º – 180º	Пд С	ІІ	-	+
180º – 270º	Пд З	ІІІ	-	-
270º – 360º	Пн З	ІV	+	-

Обернена геодезична задача полягає в тому, що, маючи координати двох точок, визначають довжину і напрямок лінії між цими точками. Обернена геодезична задача визначається за формулами

r = arc tg r

3.1.3. Послідовність камеральної обробки матеріалів теодолітної зйомки

Після виконання польових робіт проводиться обробка матеріалів польових вимірювань у камеральних умовах. Обробку матеріалів необхідно проводити в такому порядку:

1) перевірка журналів польових записів;

2) визначення горизонтальних проложень ліній;

3) визначення недоступних відстаней;

4) складання схем теодолітних ходів і урівнювання кутів;

5) визначення дирекційних кутів (азимутів);

6) визначення румбів;

7) визначення та урівнювання приростків координат;

8) визначення координат;

9) складання плану теодолітної зйомки.

Під час перевірки журналів польових записів виявляють прорахунки, описки, записують середне значення кутів і довжин ліній чорнилом і складають схему ходів.

3.1.4. Обробка кутових вимірювань у теодолітних ходах

У геометрії відомо, що теоретична сума кутів багатокутника

а_п = а_п-1 +180º - β_п;

де: п – число кутів ходу.

Проте практичне вимірювання кутів теодолітом супроводжується низкою помилок, що призводить до деякого відхилення від суми виміряних кутів Σ β_пр від теоретичної вимоги; це відхилення називають кутовою нев’язкою

f_пр = Σ β_пр - Σ β_теор

або f_пр = Σ β_пр - 180º (п – 2) – для замкнутого ходу

Для розімкнутого ходу

f_β = Σ β_прав – (а _П – а_К + п 180º) для виміряних по ходу правих кутах

f_λ = Σ λ_лів – (а _К – а_П + п·180º) для виміряних по ходу лівих кутах

Ця нев’язка не має перевищувати граничну величину, яку визначають за формулами: для

1-мінутного теодоліта ∆β = ± 1,5’ √ n

30-секундного теодоліта ∆β = ± 1’ √ n

де: n – число кутів ходу.

У тому випадку, коли кутова нев’язка виявиться допустимою, тобто меншою від граничної або рівною їй, її як поправку розподіляють на виміряні кути. Можна вважати, що всі кути вимірюють з однаковою точністю, тому кутову нев’язку треба поділити на число виміряних кутів і визначену поправку внести в кожний кут з оберненим знаком нев’язки. Під час такого розподілу кожен виправлений кут матиме дробове значення мінут, що може бути незручним за подальших обчисленнях. Звичайно кутову нев’язку розподіляють простіше: насамперед, вводять поправки в кути з дробовими частками мінут так, щоб округлити їх до цілих мінут. Решту нев’язки розподіляють по мінуті на кути, обмежені коротшими сторонами, або з усіх перелічених вище помилок в цьому випадку особливо позначиться вплив неточного центрування інструменту або встановлення віхи над точкою наведення.

3.1.5. Визначення дирекційних кутів та румбів сторін теодолітного ходу

Після ув’язки виміряних кутів починають обчислювати дирекційні кути сторін теодолітного ходу. У замкненому теодолітному ході АВСDF (рис. 43 а) праві кути β₁, β₂, ...β₅ виправлено.

Якщо через кожну з вершин ходу АВСDF провести прямі; паралельні осьовому меридіану, тоді а₁, а₂, ...а₅, будуть дирекційні кути, які треба обчислити для розв’язування прямої геодезичної задачі. Дирекційний кут однієї з сторін, наприклад АВ, має бути відомий. Якщо він дорівнює а_1, то, продовживши пряму АВ, матиме

а₂ = а₁ + 180º - β_3;

а₄ = а₃ + 180º - β_4.

У загальному виді формулу для обчислення дирекційних кутів сторін ходу можна написати так:

а_п = а_п-1 +180º - β_п;

тобто дирекційний кут лінії наступної лінії дорівнює дирекційному куту даної лінії плюс 180º і мінус кут, вправо за ходом лежачий між ними лініями: та

а_п = а_п-1 + λ_п – 180

– для лівих по ходу кутів

Рис. 43 а. Визначення дирекційних кутів

3.1.6. Обчислення та урівнювання приростків координат

Як випливає з прямої геодезичної задачі (рис. 42) прирости координат вираховують за формулами:

∆ х = d cos r

∆ y = d sin r

d – горизонтальне положення ліній;

r – градусна величина румба.

Знаки приростів координат визначають у згідно з даними табл.1.

Після обчислення приростів координат знаходять fx fy нев’язки ходу по вісях координат за формулами:

f_x = ∑ ∆ х – (х_к – х_п)

f_y = ∑ ∆ у – (у_к – у_п),

де: х_{п ,} у_п х_к , у_к – координати початкової та кінцевої точок розімкненого теодолітного ходу.

У замкненому теодолітному ході теоретична сума приростів = 0, нев’язки обчислюються за формулами:

f_x = ∑ ∆ х

f_y = ∑ ∆ у.

Абсолютна лінійна нев’язка характеризує собою величину похибок кутових і лінійних вимірювань, визначається за формулою

Після обчислення лінійної нев’язки знаходять відносну нев’язку ходу:

^,

Р – периметр ходу, тобто його загальна довжина.

Якщо f_відн не перевищує 1:2000, вимірювання якісне – виконують зрівнювання приростів координат, яке полягає у введенні в них відповідних поправок.

Поправки знаходять шляхом розподілення нев’язок f_x, f_у з протилежним знаком пропорційно до довжин сторін і вираховують виправлені прирости.

3.1.7. Обчислення координат точок теодолітних ходів

На заключному етапі координати усіх точок теодолітного ходу обчислюють за формулами:

Х_і+1 = Х_і + ∆ х_і, У_і+1 = У_і + ∆ у_і.

При цьому починають з вихідної точки теодолітного ходу і, послідовно від точки до точки, приходять до кінцевої точки, контролем є збіг обчислених координат кінцевої точки з їхніми відомими значеннями.

У замкненому ході початкова і кінцева точки співпадуть.

browser does not support the video tag.
	https://www.youtube.com/watch?v=0hmuu4FfbGY&list=PLgQx6_PuCWWNIaaFyVsvh1-bKsHcSkeoR&index=5

3.1.8. Складання плану теодолітної зйомки

Рис. 43 б. Побудова координатної сітки

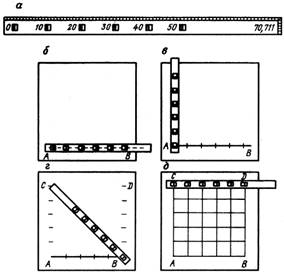
Плани викреслюють на доброму креслярському папері; розмір аркуша залежить від розміру ділянки і вибраного масштабу плану. Під час побудови плану за координатами опорних точок насамперед треба побудувати координатну сітку. Для цього застосовують спеціальну лінійку Дробишева. Це металева лінійка з шістьма вирізами по середині. Один з країв кожного вирізу скошений: у першого вирізу, позначеного нулем, – по прямій лінії, а в усіх інших – по дугах кіл з радіусами 10, 20, 30, 40, 50 см від початкового штриха. Кінець лінійки скошено по дузі радіуса 70,711 см.

Цією лінійкою можна побудувати координатну сітку на площі квадрату з стороною 50 см, а також на площі прямокутника з сторонами 30, 40 см і діагоналлю 50 см.

Порядок побудови координатної сітки зображено на (рис. 43 б).

Координатну сітку слід будувати дуже точно, тому що помилки в сітці позначаються під час побудови плану. Для контролю побудови сітки перевіряють вимірником рівність діагоналей усіх квадратів.

Побудова плану. Якщо координати обчислюють від умовного початку х = 0,

у = 0 і їх значення невеликі, то одну з вертикальних ліній сітки беруть за вісь Х, а одну з горизонтальних – за вісь У. У їх перетині х=0, у=0, намічаючи початок координат, враховують розмір плану і призначають початковими такі лінії сітки, за яких точки з найменшими і найбільшими значеннями координат розмістяться в межах сітки координат, а план – у центрі аркуша.

Якщо координати обчислено в загальнодержавній системі, то для лівої крайньої вертикальної лінії беруть значення ординати, близьке до найменшого значення ординати точки ходу, а нижній горизонтальній лінії приписують абсцису, близьку до найменшої абсциси ходу.

Наприклад:

треба побудувати план теодолітного ходу MNPK (рис. 44) в масштабі 1:5000; у цьому випадку сторона 10-сантиметрового квадрата відповідатиме 500 м на місцевості. Точка N має найменшу абсцису +7241,16; точка К – найбільшу +7870,62. точка М – має найменшу ординату +4250,70; точка Р – найбільшу ординату +5127,41.

Щоб нанести точки з зазначеними ординатами, треба отцифрувати координатну сітку.

Для нанесення точки за координатами на план спочатку потрібно визначити, в якому квадраті вона розміститься. Точка N має координати х_N = 7241,16 м, у_N = 4535,50 м. По осі Х вона має міститься в першій нижній смузі квадратів між підписами абсцис сітки 7000 і 7500; по осі У – в середній вертикальній смузі між підписами ординат сітки 4500 і 5000. Отже, точка N має бути в квадраті, розміщеному в перетині зазначених смуг.

Щоб побудувати ординату точки N, треба на верхній і нижній сторонах квадрата відкласти вправо – на схід – від лінії 4500 відрізки 35,50 м і вліво – на захід – від лінії 5000 відрізки 464,50 м.

Точки, нанесені на протилежних сторонах квадрата, сполучають прямими тонкими лініями, в їх перетині буде шукана точка N. Координати точки М будуть х_М = 7322,00 і у_М = 4250,70. вона міститься в нижньому лівому квадраті сітки. Її та інші точки ходу наносять так само, як точку N. Правильність нанесення точок перевіряють і за горизонтальними проєкціями довжини ліній між цими точками. При цьому треба розхилом вимірника брати відстань і звіряти з планом. Найбільше відхилення не має перевищувати 0,2 мм.

Потім відносно відомих ліній і точок, керуючись абрисом, наносять на план подробиці, зняті на місцевості. Способи нанесення контурних точок такі самі, як були застосовані для їх зйомки на місцевості. Проте діють при цьому в зворотному порядку.

Рис. 44. Накладання точок по їх прямокутних координатах

Наприклад, якщо від якоїсь точки теодолітного ходу полярним способом знято контур луки, то на плані при даній точці транспортиром будують відповідні кути і відкладають виміряні відстані. Далі, сполучивши знайдені точки, утворюють контур луки в даному масштабі.

browser does not support the video tag.
	https://www.youtube.com/watch?v=wAaLIBhY-24&list=PLgQx6_PuCWWNIaaFyVsvh1-bKsHcSkeoR&index=10

browser does not support the video tag.
	https://www.youtube.com/watch?v=EYlH6NRVZWk&list=PLgQx6_PuCWWNIaaFyVsvh1-bKsHcSkeoR&index=11

	ПРЕЗЕНТАЦІЯ
	Питання для самоперевірки
1. Яка послідовність камеральної обробки матеріалів теодолітної зйомки? 2. Як визначити кутову нев’язку у замкненому теодолітному ході? 3. Як визначити кутову нев’язку у розімкненому теодолітному ході? 4. Які критерії встановлення допустимої кутової нев’язки і як вона обчислюється? 5. Як обчислити дирекційні кути та румби сторін теодолітного ходу? 6. Як обчислити прирости координат та нев’язки в приростах координат в замкненому та розімкненому теодолітних ходах? 7. Як визначити лінійну та відносну нев’язку ходу? Який критерій їх допустимості? 8. Як виконати розподіл нев’язок в приростах координат? 9. Як обчислити координати вершин теодолітного ходу? 10. Суть прямої геодезичної задачі? 11. Як відцифрувати координатну сітку? 12. Як відкладати точки на план по координатах? 13. Як нанести на план елементи ситуації? 14. Як визначаються точки на поверхні Землі? 15. Суть оберненої геодезичної задачі?

ПЕРЕВІРКА ЗНАНЬ МОДУЛЯ 3

Попередня тема

На початок

Наступна тема