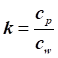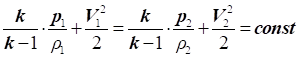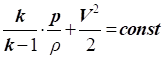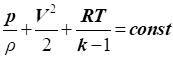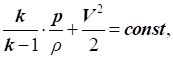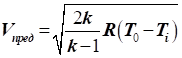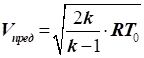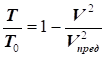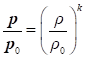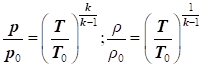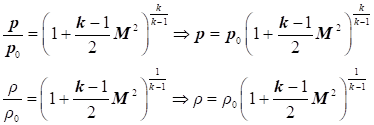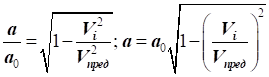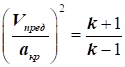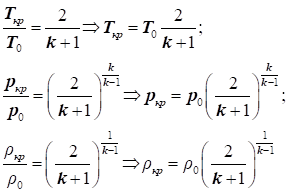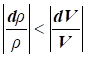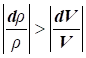|
|

|
В загальному
випадку руху газового потоку на етапах гальмування або розгону зміна
фізичних параметрів стану газу підпорядковується ізоентропічному рівнянню:
|
|
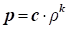 , ,
де:
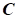 – газова постійна величина ізоентропічного процесу; – газова постійна величина ізоентропічного процесу;
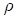 – масова
густина газу, кг/м3; – масова
густина газу, кг/м3;
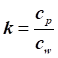 – показник
адіабати; – показник
адіабати;
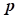 – тиск газу, Па. – тиск газу, Па.
|
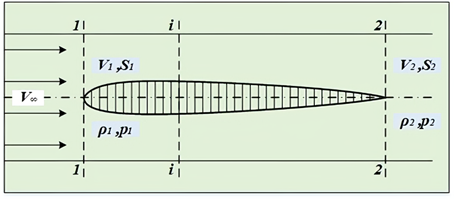
Якщо підставити
рівняння ізоентропи в рівняння Д. Бернуллі без урахування стисливості і
виконати спільне інтегрування, то отримаємо рівняння Д. Бернуллі з
урахуванням стисливості (рис. 43):
|
|
|
|
|
Рис. 43. Схема виведення рівняння
Д. Бернуллі
з урахуванням стисливості
|
|

|
У
загальному випадку рівняння Д. Бернуллі з урахуванням стисливості прийме перший вид:
|
|
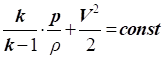
|
Рівняння
Бернуллі з урахуванням стисливості можна перетворити в інший вид,
використовуючи рівняння стану газу:
|

|
Тоді
рівняння перетворюється в другий вид
через зміну температури:
|
|
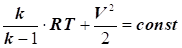
|
|

|
Можна
рівняння Д. Бернуллі перетворити в третій
вид через зміну швидкості звуку: 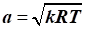
|
|
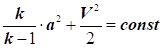
|
Так як в
адіабатичному процесі за зміни тиску стиснення газу відбувається і зміна його
температури то, отже, відбувається і зміна внутрішньої енергії газу
пропорційно 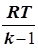 . Тоді в
рівнянні Д. Бернуллі з'являється новий член, що враховує внутрішню енергію
газу. . Тоді в
рівнянні Д. Бернуллі з'являється новий член, що враховує внутрішню енергію
газу.
|

|
Таким
чином, враховуючи що 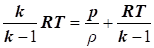 , отримаємо четвертий вид рівняння: , отримаємо четвертий вид рівняння:
|
|
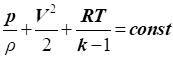
|
|
|
|
Фізична сутність рівняння
Бернуллі для стискуваного газу полягає в такому: сума потенційної енергії 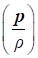 , кінетичної енергії , кінетичної енергії 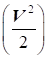 і внутрішньої енергії і внутрішньої енергії 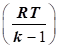 одиниці маси газу в будь-якому
поперечному перерізі струменя газу є величиною постійною одиниці маси газу в будь-якому
поперечному перерізі струменя газу є величиною постійною
|
|
|
|
|
|
|
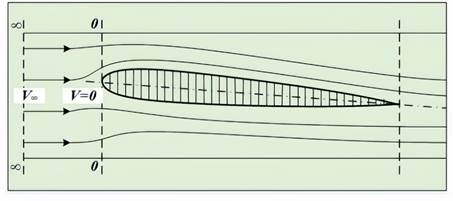
Залежність фізичних параметрів потоку від швидкості
його руху
Температура
загальмованого потоку (рис. 44):
На передній
кромці обтічних тіл завжди є область або точка, в якій газ повністю
гальмується і швидкість обтікання стає рівною «0»
(V = 0). Цю
область або точку називають критичною.
|

|
Якщо
проаналізувати рівняння Бернуллі, то можна зробити висновок, що:
|
|
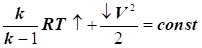
|
|
|
|
|
|
Рис. 44. Схема виведення рівняння повного гальмування
|
Звідси випливає,
що при гальмуванні потоку його температура збільшується і максимальне
значення температури буде відповідати швидкості V = 0 (тобто в точці гальмування).
|

|
Згідно
з рівнянням Д. Бернуллі, температуру загальмованого потоку можна визначити
за формулою:
|
|
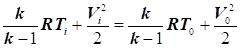 , звідси при V0 = 0, , звідси при V0 = 0,
з урахуванням рівняння 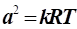 , отримаємо новий вираз визначення температури
загальмованого потоку: , отримаємо новий вираз визначення температури
загальмованого потоку:
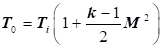
|
|

|
З цього виразу випливає, що температура загальмованого
потоку збільшується зі зростанням числа Маха (М), це пояснюється тим, що за адіабатичного гальмування
кінетична енергія потоку перетворюється у внутрішню енергію газу і йде на
збільшення його температури. Це
явище називається кінетичним
нагріванням.
|
|
|
|
Залежність
температури загальмованого потоку від чисел М:
|
M
|
0
|
1
|
2
|
3
|
4
|
5
|
|
|
288
|
346
|
518
|
807
|
1210
|
1764
|
Якби не було
теплопередачі, то температура газу в критичних точках профілів обтічних тіл
дорівнювала б температурі  газу газу а так як вона випромінюється в середовище і
розсіюється, відбивається від поверхні тіла, а також відводиться всередину
тіла, то температура в точці гальмування буде значно меншою температури
гальмування. а так як вона випромінюється в середовище і
розсіюється, відбивається від поверхні тіла, а також відводиться всередину
тіла, то температура в точці гальмування буде значно меншою температури
гальмування.
|
|
|

|
Задачі
|
|
|
1) Визначити температуру загальмованого повітряного потоку для чисел Маха М = 3 і 6, якщо політ
здійснюється на висоті
польоту Н
= 5000 м.
2) Визначити швидкісний і повний тиск на визначеній висоті,
якщо температура повітря складає мінус
250С, а число Маха М
= 0,95.
3) Визначити приладову і повітряну швидкість, а також число
Маха, якщо швидкість звуку на висоті польоту ан = 320 м/с, повний тиск повітряного потоку p* = 9,9 × 105 Па.
4) Літак летить на висоті Н = 8000 м з швидкістю V = 420 км/год. Яку швидкість буде показувати прилад
показника швидкості, якщо шкала приладу відградуйована на висоту Н = 0 м. Визначити число Маха
і температуру повітря за зазначеними вихідними даними.
Гранична
швидкість руху
|

|
Згідно
з рівнянням Д. Бернуллі з урахуванням стисливості середовища:
|
|
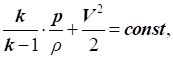 або або 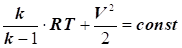
збільшення швидкості потоку газу,
а отже, збільшення його кінетичної енергії може відбуватися тільки за
рахунок зменшення потенційної енергії потоку.
|
Граничне
значення швидкості потоку настає тоді, коли потенційна енергія потоку
знижується до «0», тобто
коли відбувається зменшення абсолютної температури газового середовища до 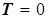 . .
|

|
Швидкість,
досягнута газовим потоком за температури середовища Т0 = 0, називається граничною і визначається за
формулою:
|
|
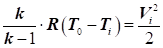 , звідси , звідси 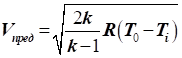
|
Якщо газ
з параметрами стану 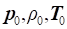 находиться
в стані спокою (наприклад, газ в балоні під тиском або пороховий двигун зі спресованим
пороховим зарядом), а потім починається витік газу з безперервним збільшенням
швидкості від находиться
в стані спокою (наприклад, газ в балоні під тиском або пороховий двигун зі спресованим
пороховим зарядом), а потім починається витік газу з безперервним збільшенням
швидкості від 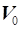 до до 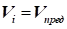 , тоді
рівняння Бернуллі приймає вигляд (рис. 45). , тоді
рівняння Бернуллі приймає вигляд (рис. 45).
|
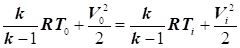 , при , при 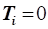
отримаємо: 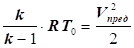 , звідси: , звідси:
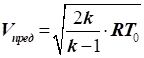
для повітря, коли 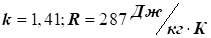 , тоді гранична швидкість дорівнює: , тоді гранична швидкість дорівнює:
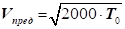 ; ;
|
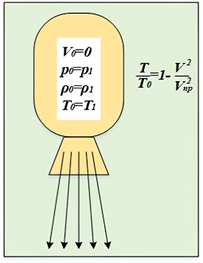
наприклад,
пороховий двигун прискорювача:
|
|
|
|
|
Рис. 45. Схема витікання газу з
порохового двигуна у вакуум
|
|

|
З
основного рівняння Д. Бернуллі можна визначити відносну зміну температури
залежно від відносної зміни швидкості потоку газу:
|
|
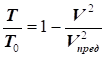
|
Задача
Визначити граничну швидкість повітряного потоку під час
польоту на висоті Н = 10000 м,
число Маха М = 2.
Тиск
і масова густина повітря
Зміна
тиску і густини рухомого газу можна виразити через зміну температури.
Використовуючи рівняння ізоентропічного процесу
|
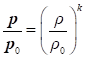
і підставивши в нього рівняння стану середовища,
отримаємо нове рівняння через зміну температури:
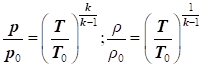
|
|

|
Потім,
якщо підставити їх у вихідне рівняння зміни температури під час гальмування
потоку, отримаємо нове рівняння визначення температури:
|
|
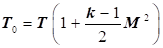
|
|

|
З
урахуванням цих перетворень отримаємо формули для визначення інших
параметрів газу з урахуванням стисливості (рис. 46):
|
|
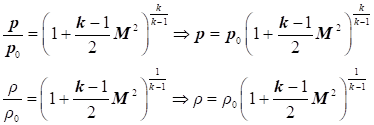
|
|
|
|
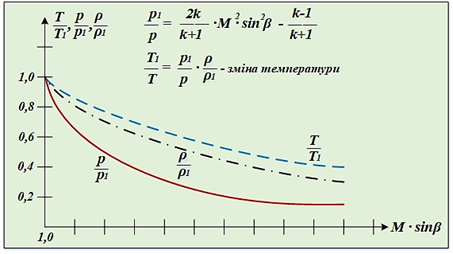
|
|
Рис. 46. Схема графіків
залежностей основних параметрів потоку
від числа Маха (М)
|
Зі збільшенням
швидкості повітряного потоку відбувається зменшення швидкості звуку в ньому.
|

|
Так
як швидкість звуку зменшується через зменшення температури потоку Т, а самє 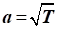 ,
то можна установити залежність між швидкістю звуку і граничною швидкістю
потоку: ,
то можна установити залежність між швидкістю звуку і граничною швидкістю
потоку:
|
|
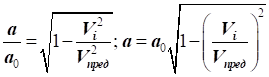
|
|
|
|

|
Задачі
|
|
|
1) Визначити швидкість звуку,
число Маха, швидкісний і повний тиск потоку, що обтікає літак в польоті зі
швидкістю V = 480 км/год на
висоті H = 5000 м, якщо
атмосферний тиск на цій висоті складає 54052
Па.
2) Визначити фактичну висоту польоту літака, приладову
швидкість, швидкість звуку і швидкісний
напір, якщо прилад
числа Маха показує значення М = 0,9,
а повітряна швидкість літака Vпн
= 980 км/год.
По мірі зростання
швидкості потоку і зменшення швидкості звуку їх значення поступово
зближуються і в деякому перерізі профілю, приблизно в місці максимальної його
товщини, вони зрівнюються. Цей переріз називається критичним (рис. 47).
|
|
|
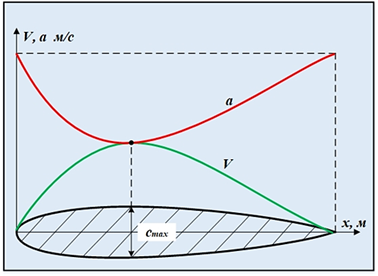
|
|
Рис. 47. Схема досягнення
швидкості звуку в критичному перерізі
|
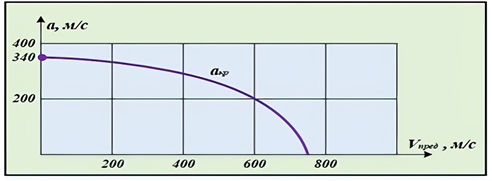
Наскільки
близькі 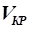 і і 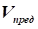 простежимо на рівнянні Д. Бернуллі, простежимо на рівнянні Д. Бернуллі,
запишемо
рівняння Д. Бернуллі для критичного перерізу, де
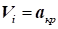 , а
швидкість при цьому дорівнює граничній , а
швидкість при цьому дорівнює граничній 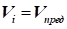 , тоді , тоді 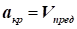 (рис. 48). (рис. 48).
|

|
Рівняння
Бернуллі для стискуваного потоку через швидкість звуку, коли: 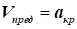 ,
має вигляд: ,
має вигляд:
|
|
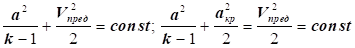 , тоді отримаємо , тоді отримаємо 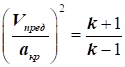
|
|
|
|
|
|
Рис. 48. Залежність швидкості звуку від граничної швидкості
потоку
|
Для повітря: 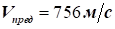 , при , при 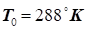
|

|
Так
як за критичної швидкості руху 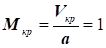 ,
то критичні значення параметрів потоку можна визначити за формулами: ,
то критичні значення параметрів потоку можна визначити за формулами:
|
|
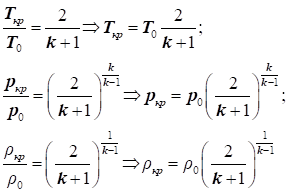
Для повітря, при 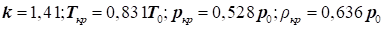 , ,
де:
T0, p0, ρ0 – фізичні
параметри повітря за усталеного руху;
Tкр, pкр, ρкр – фізичні
параметри повітря в критичному перерізі потоку.
|
|
|
|

|
Задача
|
|
|
Визначити критичні параметри повітряного потоку:
температуру, тиск і масову густину за спрощеними формулами, якщо політ літака
здійснюється на висоті Н = 2000 м.
|
|
|
|
|
Рис. 49.
Схема потоку рідини з урахуванням стисливості
|
|

|
У загальному випадку з
урахуванням стисливості рівняння Л. Ейлера має вигляд:
|
|
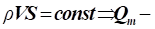 масова витрата масова витрата
|
В умовах,
коли проявляється стисливість газу, для визначення залежності між зміною
площі поперечного перерізу, масовою щільністю і швидкістю потоку газу
перетворимо рівняння у вид:
З цієї залежності
випливає, що зміна швидкості обумовлена зміною площі поперечного перерізу
струмка і зміною густини газу.
|

|
Використовуючи
співвідношення:
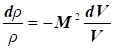 , ,
можна
зробити наступні основні висновки:
|
|
1) зміна густини і швидкості мають різні знаки: при гальмуванні
газ ущільнюється, а при розгоні – розріджується;
при 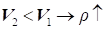 ; при ; при 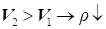
2) відносна зміна густини потоку при зміні швидкості
пропорційна квадрату числа Маха 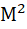 ; ;
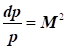
3) за швидкості потоку, меншій швидкості звуку 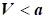 , темп зміни густини ρ газу менше темпу зміни швидкості V: , темп зміни густини ρ газу менше темпу зміни швидкості V:
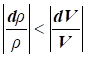
|
За
швидкості, більшій
швидкості звуку 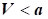 , темп зміни густини ρ газу набагато більший темпу зміни швидкості V: , темп зміни густини ρ газу набагато більший темпу зміни швидкості V:
Таким чином, при досягненні потоком газу в процесі розгону
швидкості, яка дорівнює швидкості звуку, настає якісна зміна співвідношення
між відносною зміною швидкості і відносною зміною густини газу в струминках.
|

|
З
огляду на співвідношення:
|
|
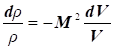
можна отримати рівняння усталеної масової витрати з урахуванням
стисливості в диференційній формі:
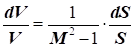
|
|
|
|

|
Задача
|
|
|
Визначити як зміниться швидкість польоту літака при зміні
висоти від Н1 = 8000 м
до Н2 = 3000 м
при незмінній вазі літака G = 100
кН і площі крила S = 150 м2,
коефіціент підйомної сили Сya
= 0,9.
|

|
З
рівняння нерозривності з урахуванням стисливості газу записаних у вигляді:
|
|
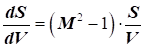
випливають
певні закономірності:
1) за дозвукової
течії газу 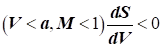 , зв'язок між змінами площі поперечного перерізу струминки
і швидкості потоку принципово такий самий, як і у нестисливої рідини: газ
розганяється в звужувальній і гальмується в розширювальній частині
струминки, проте кількісні співвідношення то більше, що більше число Маха М
потоку; , зв'язок між змінами площі поперечного перерізу струминки
і швидкості потоку принципово такий самий, як і у нестисливої рідини: газ
розганяється в звужувальній і гальмується в розширювальній частині
струминки, проте кількісні співвідношення то більше, що більше число Маха М
потоку;
2) досягнення швидкості
звуку можливо в найвужчому
перерізі,
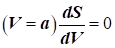 
3) за надзвукової течії 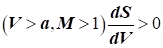 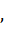 залежність
зворотна: газ розганяється в розширювальній частині струминки і гальмується
в звужувальній. Це пояснюється різкішим падінням густини в порівнянні з
приростом швидкості; залежність
зворотна: газ розганяється в розширювальній частині струминки і гальмується
в звужувальній. Це пояснюється різкішим падінням густини в порівнянні з
приростом швидкості;
4) щоб швидкість потоку збільшилася від дозвукової до
надзвукової, необхідно спочатку струмінь звужувати, поки газ не збільшить
свою швидкість до 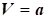 , а потім площу
поперечного перерізу необхідно розширювати для отримання надзвукової течії. , а потім площу
поперечного перерізу необхідно розширювати для отримання надзвукової течії.
|
Ці закономірності використовуються для отримання
надзвукових потоків газу за допомогою спеціально спрофільованих пристроїв, де
вхідна частина звужується, а вихідна – розширюється. Такі пристрої
називаються соплами Лаваля,
за ім’ям шведського інженера, який вперше застосував їх для отримання
надзвукової течії без суттєвої затрати енергії.
|

|
Швидкість потоку, що дорівнює місцевій швидкості звуку,
називається критичною, переріз
струменя, де досягається критична швидкість, називається критичним.
|
Теорія
сопла Лаваля
|

|
Для
аналізу умов витрати газу по трубці потоку зручно використовувати рівняння
питомої масової витрати газу:
|
|
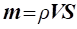 або або 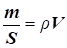
|
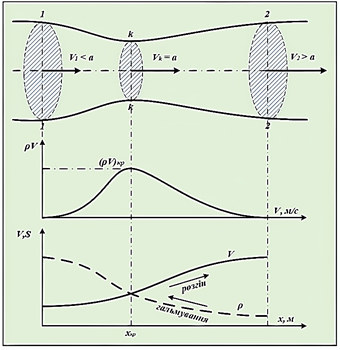
Розглянемо
зміну параметрів газу по довжині сопла Лаваля (рис. 50):
|
|
|
Окремі
випадки розв'язування рівняння:
|
1) за
відсутності швидкості руху потоку питома витрата дорівнює нулю:
2) за
швидкості потоку 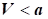 : збільшення швидкості течії газового потоку можливе
за зменшення площі поперечного перерізу: : збільшення швидкості течії газового потоку можливе
за зменшення площі поперечного перерізу: 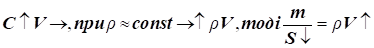 швидкість течії газового потоку досягає
значення швидкості звуку швидкість течії газового потоку досягає
значення швидкості звуку 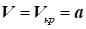 за мінімальної площі перерізу за мінімальної площі перерізу 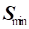 : :
3) за
швидкості потоку 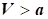 : подальше збільшення швидкості надзвукового потоку
(V >
a) можливе за розширення вихідного перерізу газового потоку через різке зменшення масової
густини газу: : подальше збільшення швидкості надзвукового потоку
(V >
a) можливе за розширення вихідного перерізу газового потоку через різке зменшення масової
густини газу:
|
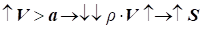 , , 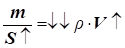
|
|
|
|
Основні
закономірності течії газового потоку в соплі Лаваля:
|
1) При 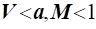 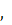 зв'язок між зміною площі перерізу струменя і швидкістю течії аналогічний, як і для нестисливого потоку: зв'язок між зміною площі перерізу струменя і швидкістю течії аналогічний, як і для нестисливого потоку:
2) При 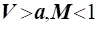 спостерігається зворотна залежність: спостерігається зворотна залежність:
|
|
|
|
|
Рис. 50. Схема зміни параметрів
потоку по довжині сопла Лаваля
|
3) Щоб збільшити швидкість потоку від дозвукової до
надзвукової необхідно:
– спочатку
звужувати поперечний переріз струменя до тих пір, поки швидкість потоку не
досягне швидкості звуку;
– потім
розширювати переріз
струменя, що призведе до ще більшого збільшення надзвукової швидкості
газового потоку.
|
|
|
Сопло
Лаваля застосовується в авіаційній техніці:
|
– у
вигляді соплових апаратів реактивних двигунів;
– в
аеродинамічних трубах для отримання надзвукових швидкостей течії під час
досліджень.
|

|
Питання для
самоконтролю
|
|
1. Рівняння Д.
Бернуллі рухомого газового потоку з врахуванням стисливості, його фізична
сутність і практичне використання.
2. Залежність
температури загальмованого газового потоку від швидкості руху, фізична
сутність кінетичного нагрівания поверхні обтічного тіла.
3. Охарактеризувати
граничну швидкість газового потоку і її залежність від температури
навколишнього середовища.
4.
Охарактеризувати критичний переріз потоку, його сутність і визначення
критичних параметрів газового потоку.
5. Рівняння Л.
Ейлера з врахуванням стисливості газу, його фізична сутність і практичне
використання.
6.
Охарактеризувати критичну швидкість стисливого газового потоку, основні
закономірності за розгону потоку від дозвукової швидкості до надзвукової.
7. Сутність
сопла Лаваля, охарактеризувати залежність параметрів газового потоку від
швидкості руху і зміни основних параметрів газового потоку по довжині сопла
Лаваля.
|
|
|
|