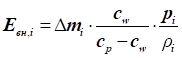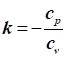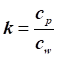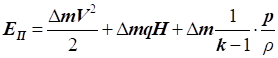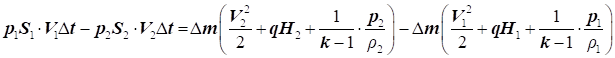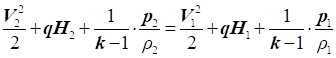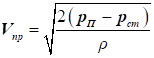|
|
|
ОСНОВИ
АЕРОДИНАМІКИ ТА ДИНАМІКИ ПОЛЬОТУ частина І АЕРОГІДРОГАЗОДИНАМІКА Електронний посібник |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1. ТЕОРЕТИЧНІ
ОСНОВИ ДОЗВУКОВОЇ ТА НАДЗВУКОВОЇ АЕРОГІДРОГАЗОДИНАМІКИ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Місце теорії у вивченні навколишнього середовища
Яка ж роль теорії в пізнанні навколишнього середовища? По-перше, теорія повинна об'єднувати сукупність явищ,
приводячи їх до деякого простішого вигляду, який дозволяє застосування
математичного методу досліджень. По-друге, теорія дає можливість проводити різні практичні
розрахунки і визначати, наприклад, раціональні форми, компонування і розміри
сучасних ЛА, а також призначення і склад авіаційного обладнання і
озброєння. По-третє, правильна теорія відображає об'єктивну істину і
тому її розвиток може передбачати нові явища, які ще невідомі, незнайомі і не
вивчені. Коротка характеристика розвитку теорії пізнання істини Спочатку з'явилася теорія Ісаака Ньютона, яка розглядала
середовище як дискретну структуру, що складається з окремих частинок рідини
чи газу, не зв'язаних між собою, так званих «корпускулів». Потім теорію доповнив Л. Ейлер, який запропонував
розглядати середовище суцільною ідеальною рідиною, позбавленою в'язкості і
стисливості, здатною передавати тільки нормальний тиск на поверхні обтічного
тіла. Ця теорія дозволяла скласти систему диференційних рівнянь і визначати
швидкості і тиск у будь-якій точці потоку рідини. Пізніше з'явилася теорія про в'язке середовище, запропонована
Л. Прандтлем, яка дозволила враховувати сили тертя, викликані властивістю
в'язкості і створити теорію примежового шару. В середині 20 століття з'явилася нова теорія – теорія
газів, яка була розроблена не на основі корпускулярної теорії Ньютона, а на
основі теорії надшвидкісного руху окремих частинок матерії, що пружно
вдаряються одна в одну чи в поверхню відповідно до кінетичної-молекулярної
теорії газів. Таким чином, теорія пізнання фізичних явищ і природи не
стоїть на місці, а постійно розвивається, удосконалюється і збагачується. Поняття про потік рідини і газу
Види руху рідини і газу Рух рідини характеризується напрямком і швидкістю частинок
рідини в окремих точках потоку, загальною формою і фізичними параметрами потоку.
Спостерігаючи за рухом частинок, можна переконатися, що швидкість руху в
різні моменти часу і в різних точках потоку можуть сильно відрізнятися. При
цьому методи спостереження за рухом частинок потоку рідини можуть бути
різними. В науці відомі два основних методи вивчення руху частинок
рідини і реєстрації параметрів середовища: методи Лагранжа і
Ейлера. За першим методом (методом Лагранжа) можна вибрати
в масі рідини, що рухається в потоці, одну якусь частинку і, рухаючись разом
з нею, спостерігати за її швидкістю в різних точках траєкторії і вимірювати
всі параметри стану рухомого середовища (рис. 23).
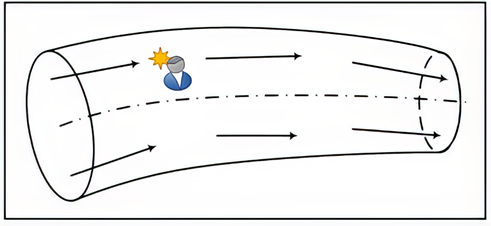
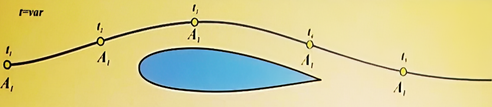
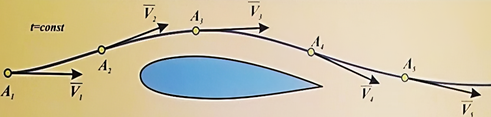
За другим методом (методом Л. Ейлера) можна
вибрати одну якусь точку поруч з
потоком і, залишаючись нерухомим, спостерігати за швидкостями різних частинок
рідини, які протікають повз цю точку, і вимірювати параметри стану рухомого
середовища (рис. 24).
Застосування методу Л. Ейлера спрощує дослідження обтікання
тіл на підставі вивчення законів руху рідин і газів відносно нерухомої точки
і дозволяє використовувати простіший апарат математичного моделювання та
аналізу. Крім цього, в рідині поряд з поступальним рухом можливі і
обертальні рухи частинок. Потік, в якому частинки рідини або газу обертаються
навколо свого центру мас (або геометричного центру) з деякою кутовою
швидкістю (
Прямолінійний рівномірний рух
рідини і газів Розглянемо виникнення швидкостей і прискорень під час
дослідження прямолінійного рівномірного руху рідини за методом Л. Ейлера
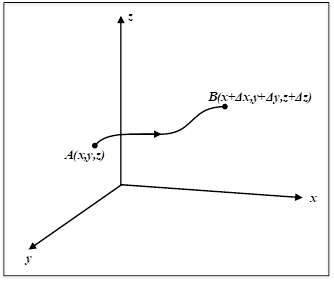
(рис. 25). Визначимо в певний момент часу (t) невеличку частинку, яка
знаходиться в т.А
з координатами (x, y, z). В момент часу (t +
Визначивши швидкості в довільній точці простору, можна зробити
висновок, що їх можна виразити у вигляді функції координат і часу (метод
Ейлера).
При переміщенні з т.А
в т.В змінюються
координати частинок рідини і газу протягом деякого часу (t), а отже, змінюються їх швидкості і
прискорення, і, як наслідок, це призведе до зміни інших фізичних параметрів
За усталеного руху потоку швидкість, тиск і густина є лише функціями
координат точки. Це означає, що через цю точку простору всі частинки потоку
проходять з однаковою швидкістю. Потік
рідини і газу характеризується певними поняттями і визначеннями, які
використовуються в аерогідрогазодинаміці. Траєкторія
Лінія
струменю
Трубка
току
Струминка
Якщо течія усталена, то конфігурація ліній струминок не
змінюється з часом і в цьому випадку лінії струминок збігаються з
траєкторією. В усталеному потоці трубка току зберігає незмінне положення в
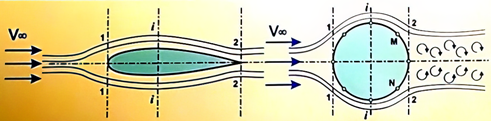
просторі. Картину, що показує розподіл ліній струминок навколо
обтічного тіла, називають спектром обтікання цього тіла. Щоб отримати спектр
обтікання дослідним шляхом, необхідно зробити видимим рух частинок рідини в
потоці. Цього можна досягти введенням в потік газу струминок диму або тонких
шовкових ниток, а в потік рідини вводять підфарбовані рідини або
використовують інші методи візуалізації потоку (рис. 29).
Поняття про обертальний рух
рідини і газу Іноді рідина приходить в обертальний рух, який називається вихровим
рухом подібно до того, як рухається вода в річкових вирах. Умови для появи вихору створюються, наприклад, за обтікання тіл з гострими
поперечними ребрами або затупленим заднім краєм. У таких випадках струминки
не можуть різко під кутом змінювати напрямок свого руху, тому з них
підсмоктується в застійні зони рідини частина потоку, з якого формуються
вихори, що зриваються з гострих кромок або областей різкої зміни напрямку
руху, які зносяться потоком. Потік рідини (газу), в якому частинки обертаються навколо
свого центру мас з деякою кутовою швидкістю ( Для теоретичних міркувань щодо впливу вихорів
використовуються основні поняття і визначення руху вихрового потоку. 1. Кутові швидкості обертання У загальному випадку частинка газу рухається, переміщається
прямолінійно, обертається навколо своєї осі і деформується. Розглядаючи рух і
обертання елементарної частинки з урахуванням деформації можна отримати
розрахункові формули для визначення кутової швидкості
Розкриваючи матрицю, можна отримати розрахункові формули для
визначення кутової швидкості в проєкціях на осі координат.
Кутова швидкість обертання частинок рідини має місце там,
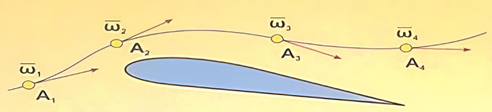
де є градієнт швидкості течії по перерізу потоку рідини. 2. Вихрова лінія, вихрова трубка, вихровий шнур 2.1. Вихровою лінією називається лінія, в кожній
точці якої в даний момент часу (t), вектор кутової швидкості обертання частинок рідини
спрямований по дотичній до неї (рис. 30).
Якщо через всі крапки замкненого контуру поперечного перерізу
вихору провести вихрові лінії, то отримаємо поверхню, що називається вихровою
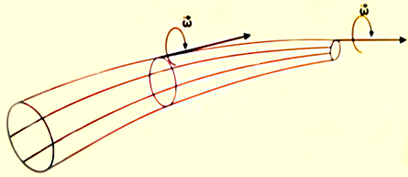
трубкою. 2.2. Вихровою трубкою називається об'ємна поверхня, яка утворена вихровими лініями, що проходять через деякий
нескінченно малий контур в просторі. Всередині вихрової трубки частинки
здійснюють обертально-поступальний рух. Ці частинки утворюють вихровий шнур
(рис. 31). 2.3. Вихровим шнуром називається частина потоку рідини, що рухається
всередині вихрової трубки. Нескінченно тонкий вихровий шнур в аеродинаміці називається
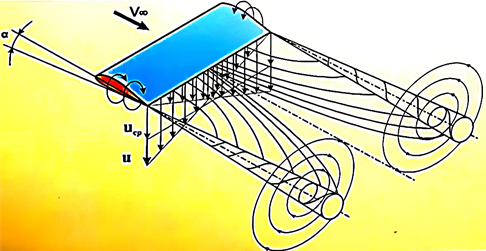
вихровою ниткою. На практиці вихрові шнури мають місце за перетікання
повітря на кінцях консолей крила з нижньої поверхні на верхню, а саме –
здійснюється перетікання повітря з області високого тиску під крилом в
область низького тиску над крилом (рис. 32). Крім цього, вихровий рух виникає
за обтікання виступаючих в потоці твердих тіл з гострими краями.
Реальні явища природи дуже складні і недоступні для суворого
теоретичного аналізу. Тому для побудови теорії того чи іншого явища
доводиться схематизувати дійсність і брати в якості об'єкта вивчення не
реальне явище, а його спрощену фізичну модель. У теоретичній аеродинаміці
протягом її розвитку було прийнято цілу низку моделей обтікання твердих тіл
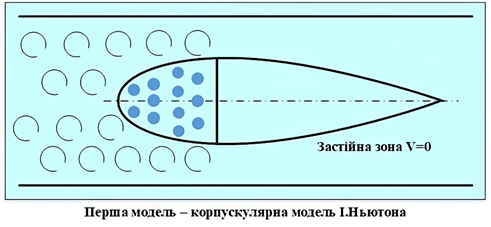
потоком повітря. 1. Перша модель (модель корпускулярної будови середовища) була запропонована Ісааком Ньютоном
(рис. 33). У цьому випадку рідина розглядається як середовище, що складається
з окремих, не пов'язаних між собою, частинок – корпускул, які під час
взаємодії з тілом повністю втрачають свою кінетичну енергію, прилипають до
нього і віддають тілу енергію у вигляді потенційної енергії сил тиску, інші
частинки проходять повз обтічне тіло і утворюють застійну зону, в якій
швидкості частинок дорівнюють нулю.
Така модель має великий недолік, тому що не розглядає обтікання
тіл і допускає велику похибку під час розрахунку сили опору в повітряному
потоці великої густини. Вона може бути застосована для розгляду явищ
обтікання твердих тіл в розрідженому середовищі. 2. Друга модель (модель ідеальної рідини).
За такої моделі, потік рідини, що обтікає тверде тіло, вважається суцільним
середовищем, позбавленим властивостей в'язкості і стисливості. Математичне
дослідження цієї моделі призвело до складання 3-х диференціальних рівнянь
руху рідини, вирішення яких дає можливість визначення швидкостей (V) і тисків (p) в будь-якій
точці потоку, що обтікає тіла.
3. Третя модель (модель стисливої рідини).
На базі цієї моделі була створена наукова школа газової динаміки, що вивчає
закони руху тіл у повітрі і газах з великими швидкостями і за високих
температур, при яких необхідно враховувати стисливість.
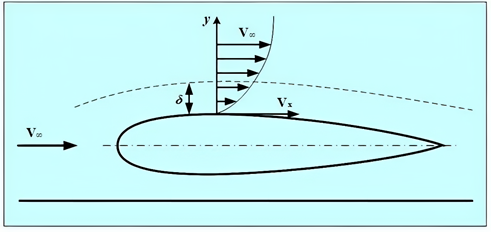
4. Четверта модель (модель в'язкої рідини).
Ця модель запропонована Л. Прандтлем, який розробив теорію примежового шару і розкрив причину виникнення сили тертя,
викликаної властивістю в'язкості (рис. 34).
5. П'ята модель (модель плазмового стану середовища), що
виникає навколо тіла, яке рухається з гіперзвуковою швидкістю. Плазма є
середовищем, що складається з суміші електрично заряджених і нейтральних
частинок. Середовище, подібне плазмі, має місце під час входу космічних
об'єктів в щільні шари атмосфери землі.
Картину, яка показує розподіл траєкторій повітряних
струминок потоку навколо обтічного тіла, називають спектром обтікання цього
тіла (рис. 35). Щоб отримати спектри дослідним шляхом, необхідно зробити
видимим рух частинок потоку. Це можна досягти введенням в потік струминок
диму, тонких ниток або шовковинок. Якщо траєкторії частинок описуються плоскими кривими, то
такий потік називається плоскопаралельним. Якщо траєкторії частинок мають
переміщення по 3-х взаємно перпендикулярних напрямках, то такий потік називають
просторовим.
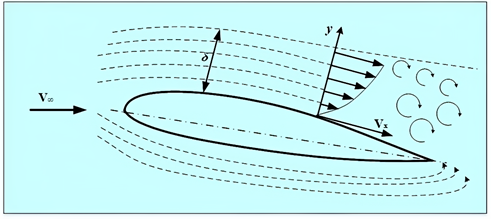
1.
Тонкий шар, що прилягає до обтічного тіла, називається примежовим
шаром. У ньому мають місце великі градієнти швидкості 2. Течії поза примежовим шаром. Градієнти швидкості в цій
зоні незначні, в'язкість слабка, сили тертя невеликі. Для спрощення досліджень за межами примежового шару середовище вважається незбуреним, ідеальним. 3. Спутний
слід – це частина повітряного потоку,
що сходить з хвостової частини обтічного тіла, в
якому течія в
основному вихрова, мають
місце великі градієнти швидкостей, проявляються властивості в'язкості і
виникають сили тертя. Вид
спектру обтікання залежить від: форми тіла, швидкості потоку, а також від
значень параметрів стану повітря, що визначають величину і характер проявів
таких його властивостей, як в'язкість і стисливість. У деяких випадках одна
або обидві ці властивості практично не проявляються і з метою спрощення
розрахунків аеродинамічних сил їх впливом можна знехтувати.
1) Визначити, як зміниться висота і швидкість польоту
літака, якщо температура повітря змінюється від + 200С на поверхні землі до мінус 450С за
бортом літака, а число Маха М = 0,6. 2) Визначити, як зміниться швидкість течії і швидкісний
тиск в струменях над і під профілем, якщо на висоті польоту Н = 5000 м за швидкості V = 720 км/год. Площа
поперечного перерізу струменю перед профілем S = 10 см2 і змінюється: над профілем
зменшується на 20%, а під
профілем збільшується на 40%. 3) Визначити число Маха і число Рейнольдса на висоті Н = 8000 м, якщо швидкість
літака V = 900 км/год, коефіцієнт динамічної в'язкості на цій висоті 1,457 * 10-5 Н
с/м2, хорда крила b = 1,5 м. 4) Визначити коефіцієнт кінематичної в'язкості повітря і
число Рейнольдса на висоті 10000 м,
якщо коефіцієнт динамічної в'язкості на цій висоті 1,457 × 10-5 Н с/м2, швидкість
літака 420 км/год, діаметр
фюзеляжу літака 5 м.
Стан газу, як робочого тіла, характеризується певними
значеннями параметрів стану: тиском (p), температурою (Т) і питомим
об'ємом (w) чи масовою густиною (ρ). Використовуючи основне рівняння молекулярно-кінетичної
теорії газів, можна встановити взаємозв'язок між параметрами ідеального газу
в будь-якому термодинамічному стані. Зміна хоча б одного із параметрів призводить до зміни інших
параметрів. У загальному вигляді зв'язок між термодинамічними
параметрами може бути представлений залежністю: f (p, T, w, ρ) = 0.
Рівняння отримано шляхом об'єднання окремих законів Бойля-Маріотта і Гей-Люссака до загального
закону і воно отримало назву рівняння Клайперона-Менделєєва.
Найбільший інтерес представляє визначення параметра за двома
іншими відомими параметрами, які можна визначити за допомогою певних
інструментальних приладів.
1) У скільки разів зменшиться об'єм газу в циліндрі поршневого
двигуна в процесі стискання, якщо перед стисканням тиск і температура
дорівнювали 2,0 кГс/см2 і +350С, а в кінці стіскання – 25 кГс/см2 і +6000С. 2) Визначити вагу повітря, что
міститься в бортовому балоні гальмівної системи вертольота, якщо об'єм балона
6 л, тиск в балоні 190 кГс/см2, а
температура + 350С. Рівняння нерозривності
рухомого потоку (рівняння Л. Ейлера) Рівняння нерозривності відображає умовне збереження маси
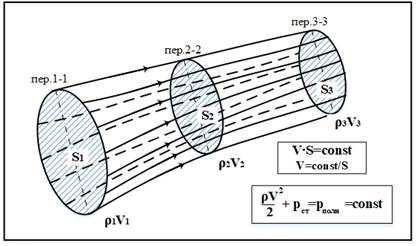
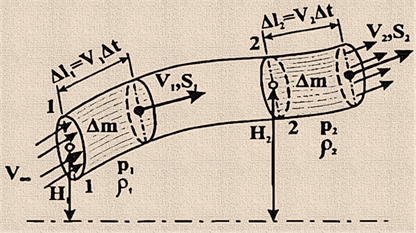
рухомого потоку рідини або газу. Для виведення рівняння віртуально виділимо в
потоці рідини або газу замкнутий об'єм у вигляді трубки току (рис. 36):
Рівняння нерозривності виведено на підставі закону збереження
матерії, установленого в 1748 р. російським вченим М. В. Ломоносовим. Рівняння
нерозривності було опубліковано Л. Ейлером у 1770 р. і є застосуванням закону
збереження енергії до струминки газу. Нехай в перерізі «1-1»
площа Через переріз «2-2»
проходить за 1 с своя маса
повітря: Так як через бічну поверхню трубки потік повітря не
просочується, то через будь-який переріз трубки за однаковий час проходить
однакова маса повітря:
Фізичний сенс
рівняння: за малих швидкостей руху повітря зменшення площі перерізу
потоку викликає збільшення швидкості руху.
З рівняння випливає, що за дозвукової швидкості потоку
швидкість руху газу в струминки обернено пропорційна площі поперечного перерізу,
тобто за зменшення площі поперечного перерізу струминки швидкість течії
зростає, і навпаки. У разі руху з великою дозвуковою, трансзвуковою і
надзвуковою швидкістю, коли проявляється властивість стисливості, зміна
швидкості залежить не тільки від площі поперечного перерізу, але і від зміни
масової густини. Тоді вираз набуде вигляду:
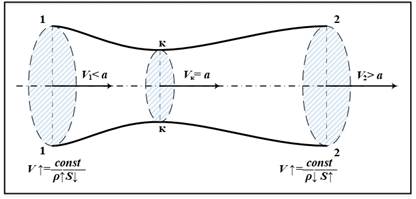
За надзвукової швидкості потоку внаслідок особливостей зміни
фізичних характеристик густина газу змінюється швидше, ніж швидкість течії.
Тому для отримання надзвукової швидкості і її збільшення необхідно
розширювати струминку, збільшувати площу її поперечного перерізу за певним
законом. Безперервне збільшення швидкості потоку від дозвукової до
надзвукової можливо лише в струминці, що має форму сопла Лаваля (рис. 37). За великих швидкостей потоку на стисливість повітря впливає
не тільки швидкість потоку, а й швидкість звуку в потоці. Як критерій
стисливості рухомого повітря використовується число Маха Таким чином, рівняння сталої витрати,
будучи відповідним вираженням закону збереження матерії стосовно струмка
газу, пов'язує між собою швидкість, масову густину і площу того поперечного
перерізу струмка, в якому розглядаються ці характеристики.
1) Визначити розмір швидкісного тиску, повний тиск і число
Маха на висоті Н = 4000 м,
за швидкості 400 км/год. 2) За обтікання крила повітряним потоком площа струменю
зменшилась у 2 рази.
Визначити швидкість струменю і швидкісний тиск у найвужчому перерізі, якщо
швидкість польоту літака 480 км/год
на рівні земної поверхні. 3)
Визначити, як зміниться розмір швидкісного тиску на елементи
конструкції літака, який летить зі швидкістю V = 720 км/год, за зміни висоти з Н1 = 2 км до
Н2 = 4000 м. 4) Визначити, як зміниться швидкість і швидкісний тиск в
струминках над і під профілем крила, якщо на висоті польоту Н = 3000 м за швидкості 320 км/год площа поперечного
перерізу струменю перед профілем S
= 50 см2 і змінюється таким чином: над профілем
зменшується на 20%, а під
профілем збільшується на 40%.
На масу газу, що знаходиться ліворуч в перерізі «1-1», діє сила тиску За переміщення газу з перерізу «1-1» до перерізу «2-2»
на відстань Δl = V1-2
× Δt сила тиску здійснює роботу ΔР × Δl,
при цьому змінюється енергія тиску, що рівносильна величині роботи, яку
здійснюють силами тиску. Різниця енергій тиску в перерізах «1-1» і «2-2» називається енергією проштовхування маси газу між
цими перерізами.
Зовнішнє тепло, що підводиться до частинки газу, витрачається
на збільшення теплозбереження, збільшення кінетичної енергії і виконання
зовнішньої роботи.
Сума внутрішньої енергії і енергії тиску газу називається
теплозбереженням або ентальпією газу: З огляду на рівняння стану газу:
враховуючи, що
де
Фізичний сенс
рівняння: зміна кінетичної енергії газу переважно відбувається за
рахунок зміни його теплозбереження. Рівняння балансу енергії
рухомого потоку (рівняння Д. Бернуллі) Рівняння Бернуллі є доповненням до закону збереження
енергії рухомих частинок рідини і газів. Цей закон сформулював відомий учений
Д. Бернуллі у 1738 році. Виділимо в усталеному потоці рідини трубку струминок. Нехай в перерізі «1-1» площею У перерізі площею Згідно з рівнянням про нерозривність потоку через виділені
перерізи потоку за час
Визначимо роботу, яку здійснюють сили тиску в рідині в
перерізі «1-1»:
аналогічно виглядає і робота для перерізу «2-2»:
Різниця виконаних робіт над об’ємом рідини між перерізами «1-1» і «2-2» буде дорівнювати:
Повна енергія маси рухомого газу включає в себе: кінетичну енергію
руху, потенційну енергію положення і внутрішню енергію:
Кінетична
енергія характеризує здатність виділеної маси газу виконувати
роботу за його гальмування від вихідної швидкості до нульового значення:
Потенційна
енергія положення характеризує енергію сили ваги газу і показує,
яку роботу маса газу
Внутрішня
енергія характеризує здатність виділеної маси газу виконати роботу
за зміни температури:
З огляду на рівняння стану газу
Тоді рівняння повної енергії маси газу в загальному вигляді
можна записати у вигляді:
Підставивши в це рівняння
З огляду на рівняння нерозривності і згрупувавши величини з
однаковими індексами, отримаємо рівняння Д. Бернуллі з урахуванням
стисливості:
Так як в аеродинаміці струминки газового потоку знаходяться
практично на одному рівні, то зміну потенціальної енергії тиску від положення
в рівнянні можна не враховувати, тобто
Якщо газ рухається з малою дозвуковою швидкістю (М ≤ 0,3), стисливістю його
можна знехтувати, тобто
У загальному вигляді рівняння Д. Бернуллі без урахування
стисливості має вигляд:
Фізичний сенс
рівняння Бернуллі полягає в тому, що за усталеного руху нестисливого газу
повний тиск дорівнює сумі статичного і динамічного тиску і є величиною
постійною у всіх перерізах одного і того ж потоку газу. Практичне використання
основних рівнянь Рівняння встановлюють дуже важливу для аеродинаміки
залежність між швидкістю потоку, тиском в ньому і основними газодинамічними
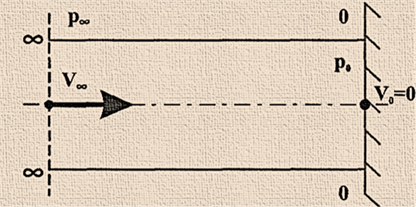
параметрами газу. Повне гальмування газового
потоку У разі повного гальмування потоку газу в перерізах
кінетична енергія рухомого газу повністю перетворюється в потенційну енергію
тиску (рис. 40).
Таким чином, у випадку повного гальмування
потоку нестисливого газу підвищення тиску в місці гальмування дорівнює
швидкісному напору, а тиск загальмованого потоку дорівнює повному тиск
1) Визначити, як зміниться повний тиск в критичній точці
носової частини фюзеляжу літака на висоті 8000 м, якщо швидкість літака змінюється від 400 до 900 км/год. 2)
Визначити температуру загальмованого повітряного потоку для чисел Маха М = 3 і 5, якщо температура набігаючого потоку t = 300С. Виникнення підйомної сили На підставі рівняння нерозривності і рівняння балансу
енергії рухомого газу можна пояснити фізичну сутність виникнення підйомної
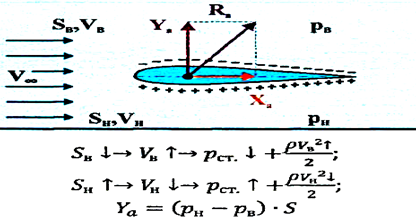
сили на твердому тілі, що обтікається потоком газу (рис. 41). При обтіканні тіла газовим потоком на верхній його поверхні
швидкість потоку збільшується через зменшення площі перерізу струмків, що
призводить до зменшення тиску. На нижній поверхні швидкість потоку
зменшується через збільшення площі поперечного перерізу струминок, що
призводить до збільшення статичного тиску. Таким чином, на обтічному тілі виникає різниця тисків, що
призводить до виникнення підйомної сили Yа,
спрямованої вгору.
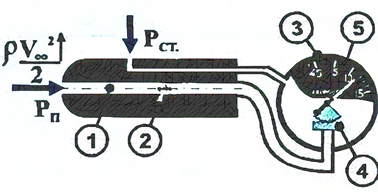
Вимірювання швидкості польоту На підставі закону Д. Бернуллі використовується принцип
вимірювання швидкості польоту літального апарату. Вимірювання швидкості
здійснюється за допомогою приймача повітряного тиску (ППТ), що складається з 2-х трубок: внутрішньої трубки 1, яка є приймачем повного
тиску, і зовнішньої трубки 2,
яка є приймачем статичного тиску (рис. 42):
Обидві трубки з'єднані з покажчиком швидкості 3, під дією різниці тисків
мембранна коробка 4
деформується і через передавальний механізм пересуває стрілку приладу 5, звідси формула для розрахунку приладової швидкості:
Швидкість, виміряна ППТ, називається приладовою швидкістю ЛА. Зі збільшенням висоти польоту,
в зв'язку зі зменшенням густини повітря, показання приладу стають
недостовірними. Тому повітряна швидкість ЛА
1) Визначити приладову і повітряну швидкість польоту літака,
якщо статичний тиск за бортом літака на заданій висоті 1,013 × 105 Па, тиск в критичній точці на
фюзеляжі літака 1,108 × 105
Па, а масова густина 0,5
кг/м3. 2) Літак летить на висоті Н = 8000 м. Яку швидкість буде показувати прилад показника
швидкості і яка буде фактична повітряна швидкість, якщо повний тиск 1,15 × 105 Па.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


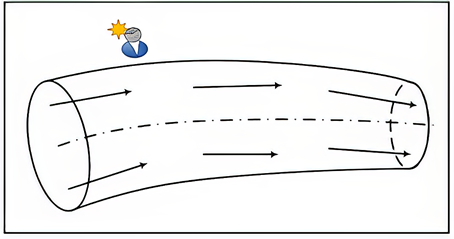

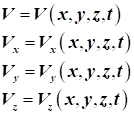
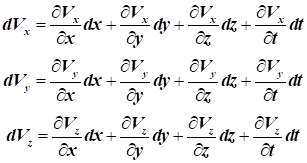

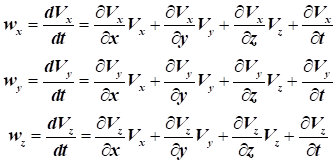
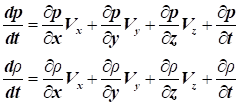

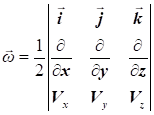
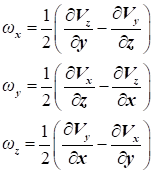

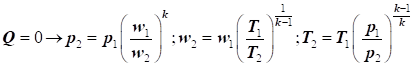
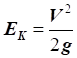 , кГс м / кг.
, кГс м / кг.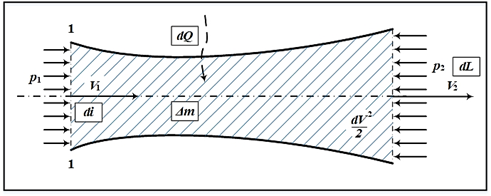
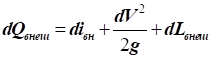 ,
,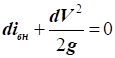
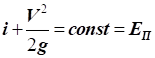
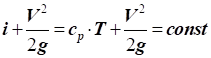
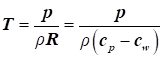 ,
,