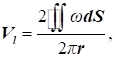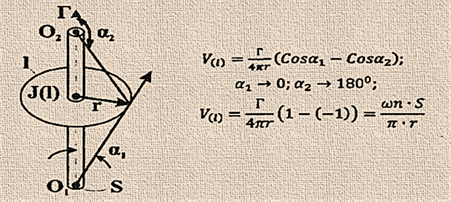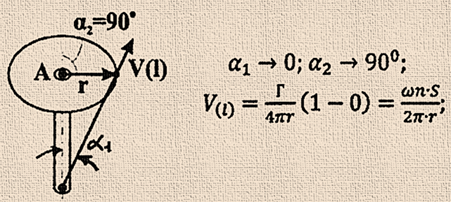ОСНОВИ АЕРОДИНАМІКИ ТА ДИНАМІКИ ПОЛЬОТУ

частина І

АЕРОГІДРОГАЗОДИНАМІКА

Електронний посібник

ГОЛОВНА	ТЕОРЕТИЧНІ ВІДОМОСТІ	АНОТАЦІЯ
ДОДАТКИ	СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

1. ТЕОРЕТИЧНІ ОСНОВИ ДОЗВУКОВОЇ ТА НАДЗВУКОВОЇ АЕРОГІДРОГАЗОДИНАМІКИ

1.4. Закономірності вихрового руху потоку. Теорема М. Є. Жуковського про підйомну силу крила

1.4.1. Закономірності вихрового руху потоку рідини і газів. Основні теореми про вихори

1.4.2. Моделювання течії газодинамічними особливостями. Теорема М.Є. Жуковського про подйомну силу

1.4.3. Фізична сутність газодинамічних особливостей і принцип моделювання потенційної течії

1.4.1. Закономірності вихрового руху потоку рідини і газів. Основні теореми про вихори

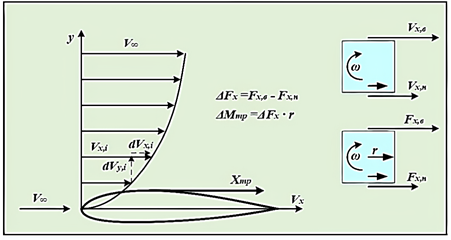
За обтікання аеродинамічних тіл повітряним потоком, швидкість течії в струминках потоку змінюється в міру віддалення від поверхні обтічного тіла. У реальному повітряному потоці відмінність швидкостей між сусідніми струминками призводить до виникнення дотичних сил тертя, розмір яких пропорційний градієнту швидкості за товщиною примежового шару повітряного потоку (рис. 51).

Рис. 51. Схема виникнення вихрового руху частинок

τ = μ _*; X_ТР = τ _* S; М_ТР = Х_{ТР *} r; ω = f (М_ТР)

Внаслідок властивостей в'язкості між шарами струминок виникають сили тертя. При цьому слої струминок з великими швидкостями захоплюють за собою уповільнені шари, а шари струминок з меншими швидкостями гальмують шари, які рухаються з великими швидкостями. У свою чергу великі швидкості викликають великі сили тертя.

Таким чином, виникає пара сил тертя, які на радіусі до центру мас частинок викликають появу моменту тертя і як наслідок призводять до виникнення обертального руху частинок, який називається вихровим рухом.

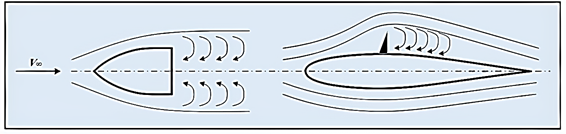
В реальному потоці вихрова течія повітря утворюється за обтікання тіл з затупленим заднім краєм або з гострими поперечними краями (рис. 52). Вихори, залежно від їх інтенсивності, під час обертання з деякою кутовою швидкістю, втягують в обертальний рух сусідні струминки рідини або газу, які були нерухомими або рухалися прямолінійно, і тим самим викликають обертальний рух в додатковій масі середовища.

Положення вихорів в просторі визначається вихровими лініями. Потужність вихорів оцінюється їх напругою (або інтенсивністю).

Рис. 52. Схема джерел вихрового руху

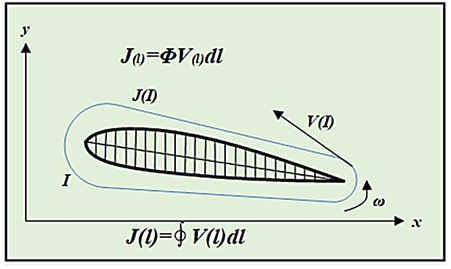
У загальному випадку напруга вихору визначається рівнянням (рис. 53):

, для загального випадку

Напругою вихору (Г) називаєють фізичну величину, рівну подвоєному подвійному інтегралу добутку кутової швидкості обертання вихору на площу поперечного перерізу вихору.

	Для окремого випадку, коли кутова швидкість постійна (), рівняння напруги вихору має вигляд:
, де: нормальна складова результуючого вектора кутової швидкості обертання вихору, ^1/c; площа поперечного перерізу вихору, м^2.

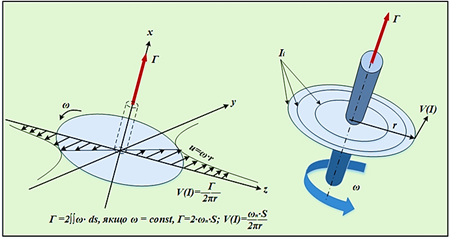
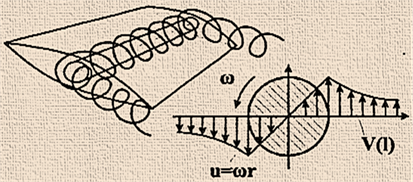
Всередині кожного вихору колова швидкість обертання частинок рідини чи газу пропорційна кутовій швидкості обертання і відстані від центру вихору до кола вихору. В навколишньому середовищі вихор збуджує обертальний рух нерухомих частинок рідини чи газу (рис. 53).

	Колову швидкість, індуковану нескінченним прямолінійним вихровим шнуром, можна визначити за формулою:
для , для де: індукована вихором колова швидкість на довільному замкнутому контурі (), м/с; колова швидкість по площі вихору, м/с.

Рис. 53. Схема виникнення індукованої вихором збуреної швидкості

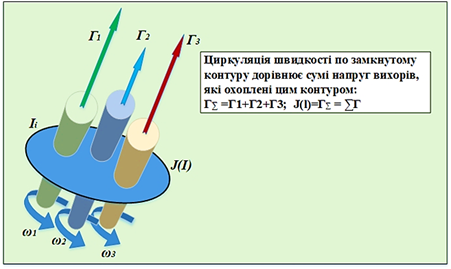
Вихровий рух характеризується поняттям циркуляції швидкості по довільному замкненому контуру (рис. 54):

Рис. 54. Схема виникнення циркуляції швидкості

по замкнутому контуру

Циркуляцією швидкості по замкнутому контуру (J(l)) називають величину, яка визначається криволінійним інтегралом добутку дотичної складової індукованої вихором швидкості на довжину замкнутого контуру.

Задачі

1) Визначити для нескінченного вихору напругу, індуктивну швидкість і колову швидкість на перерізі вихору, якщо частота обертання вихору ω_в = 25 ¹/с, площа перерізу вихору S_в = 80 см², радіус кола, що охоплює вихор, R = 40 см.

2) Визначити, як зміниться повний тиск в критичній точці носової части фюзеляжу літака за зміни висоти польоту з Н₁ = 1000 м до Н₂ = 5000 м, швидкість V = 720 км/год.

Основні теореми про вихори

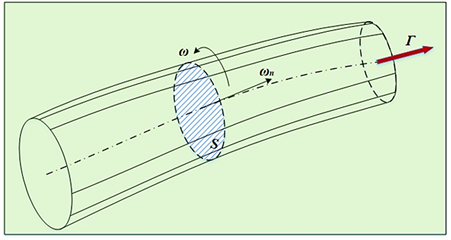
У загальному вигляді вихор характеризується певними геометричними параметрами: площею поперечного перерізу вихору і його довжиною, а також кінематичними параметрами: кутовою швидкістю обертання вихору і його напругою (рис. 55).

Рис. 55. Схема кінематичних параметрів вихору

Теорема Гельмгольца

Визначення: напруга (інтенсивність) вихору по його довжині не змінюється в часі і є величиною постійною (рис. 56):

Рис. 56. Кінематична схема вихору

В ідеальній рідині несучі поверхні можна моделювати вихорами, які дозволяють визначати збурені швидкості і тиск і, як наслідок, розраховувати аеродинамічні сили на тілі, що моделюється вихорами.

Наслідок теореми:

– вихрові шнури мають бути замкнутими по контуру;

– вихрові шнури мають спиратися на будь-які тверді поверхні;

– вихрові шнури повинні мати нескінченну довжину.

Якщо розглянути довільний замкнутий контур, то циркуляцію швидкості по цьому контуру можна представляти як проєкції результуючої циркуляції швидкості на відповідні осі координат:

Теорема Стокса

Визначення: циркуляція швидкості по замкнутому контуру () дорівнює сумарній напрузі всіх вихорів, які охоплюються цим контуром (рис. 57).

Рис. 57. Схема сумарної напруги вихорів

Теорема використовується за моделювання несучих поверхонь декількома прямолінійними вихорами, які створюють сумарну циркуляцію швидкості по довільному замкнутому контуру, що охоплює вихрові шнури.

Теорема Томпсона

Визначення: циркуляція швидкості по замкнутому контуру, що проходить через одні й ті ж точки в просторі, з часом не змінюється (рис. 58).

Рис. 58. Схема циркуляції швидкості по замкнутому контуру

Наслідок теореми:

якщо в ідеальній рідині циркуляція швидкості по замкнутому контуру з часом дорівнює нулю (тобто рух невихровий), то воно буде невихровим і в наступні моменти часу.

Задачі

1) Визначити приладову і повітряну швидкості та швидкісний тиск на висоті Н = 6000 м, якщо повний тиск p* = 1,1 × 10⁵ Па.

2) Визначити, як зміниться масова витрата повітря за швидкості V = 720 км/год на висоті Н = 3000 м за зміни діаметру повітряного потоку з d₁ = 50 см до d₂ = 0,9 м.

1.4.2. Моделювання течії газодинамічними особливостями. Теорема М. Є. Жуковського про підйомну силу

Загальне поняття про газодинамічні особливості

Поза вихровою трубкою рідина або газ знаходяться в стані спокою або прямолінійного рівномірного руху. За появи вихрового руху частинки рідини або газу, які перебували в нерухомому стані або рухалися прямолінійно, залучаються до вихрового руху залежно від величини кутової швидкості обертання і відстані від центра вихору. Згідно з теоремою Стокса циркуляція швидкості по замкнутому контуру навколо вихору дорівнює напрузі (інтенсивності) вихрового шнура.

Для вирішення практичних задач в аерогідрогазодинаміці поверхні ЛА можуть моделюватися газодинамічними особливостями, до яких відносять:

– вихори; витоки;

– стоки; диполі.

Газодинамічні особливості можуть використовуватися автономно або у взаємодії.

Сутність моделювання полягає в тому, що поле збурених швидкостей і тисків, викликаних обтічним тілом, замінюється аналогічним полем, але створюваним відповідними газодинамічними особливостями.

Моделювання несучої поверхні приєднаними вихорами

Несуча поверхня моделюється одним або декількома вихорами (рис. 59 і 60).

Рис. 59. Схема моделювання профілю несучої поверхні

приєднаними вихорами

Рис. 60. Схема моделювання лопаті несучого гвинта (НГ)

приєднаними вихорами

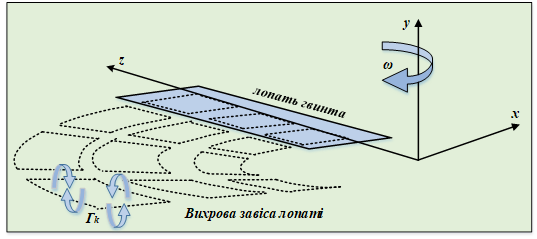
За моделювання несучих поверхонь вихровими шнурами, поверхню розбивають на рівні площадки і в кожну із них поміщають підковоподібний вихровий шнур. Вихрову пелену, що сходить з несучої поверхні, моделюють кінцями підковоподібного вихрового шнура. Вихровий шнур, обертаючись з деякою кутовою швидкістю, індукує навколо себе появу збуреної швидкості, яка згідно з рівнянням Д. Бернуллі викликає появу поля тисків і, як наслідок, виникає перепад тисків. Розглянемо фізичну сутність появи і розмір індукованої вихором швидкості.

Нехай прямолінійний вихор обертається з деякою кутовою швидкістю (ω) і має певне напруження (Г). По колу, що охоплює вихор (l), швидкість, індукована вихором, постійна в часі V(l) = const.

	Індуктивну швидкість V(l) розраховують за формулою Біо-Савара, викликану прямолінійним вихровим шнуром, що обертається з деякою кутовою швидкістю (ω) (рис. 61):

Рис. 61. Схема визначення індуктивної швидкості V(l) прямолінійного вихору за формулою Біо-Савара

З формули випливає, що колова швидкість, індукована вихором, на самому вихорі, дорівнює , а за збільшення радіуса зменшується обернено пропорційно радіусу вихору до Вздовж радіус-вектора радіальна швидкість дорівнює нулю (рис. 61).

Розглянемо випадки, коли прямолінійний вихор має різну довжину.

а) Вихор нескінченної довжини (рис. 61):

Нехай колова швидкість, індукована вихором О₁О₂, лежить в площині, перпендикулярній осі вихору, і її величину можна визначити за формулою Біо-Савара.

Для цього випадку , тоді , а , таким чином:

б) Вихор напівнескінченної довжини (рис. 62):

для цього випадку , тоді , а , отже:

Таким чином, індукована вихором напівнескінченної довжини швидкість в два рази менша, ніж швидкість, індукована вихором нескінченної довжини.

Рис. 62. Схема напівнескінченного прямолінійного вихору

Задачі

1) Визначити напругу вихору і індуковану вихором швидкість, якщо кути твірних конусу вихору α₁ = 45⁰, α₂ = 135⁰, радіус кола, що охоплює вихор, R = 30 см, число обертання вихору n_в = 335 об/хв.

2) Визначити напругу вихору, індуковану вихором швидкість для напівнескінченного вихору і колову швидкість на перерізі вихору, якщо число обертів вихору n_в = 240 об/хв, кути твірних конусу вихору α₂ = 90⁰, α₁ = 0⁰, радіус кола, що охоплює вихор, R = 100 см, площа перерізу вихору S_в = 50 см²_.

Теорема М. Є. Жуковського про підйомну силу крила

У 1906 р. М. Є. Жуковський прийшов до висновку, що в ідеальній рідині, яка обтікає циліндричне тіло нескінченного розмаху, підйомна сила може виникнути тільки за наявності циркуляції швидкості по замкнутому контуру, який охоплює обтічне тіло (рис. 63).

У запропонованій М. Є. Жуковським розрахунковій схемі профіль крила замінюється приєднаним підковоподібним вихором. Така схема дозволила побудувати математичну модель обтікання і отримати математичне рішення.

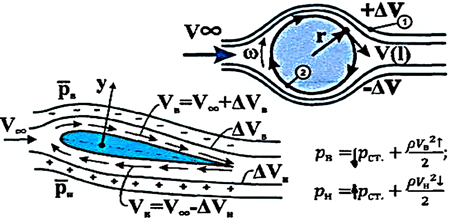
Профіль крила розглядається як обтічне тіло, навколо якого створюється циркуляція швидкості, індукована вихором.

За взаємодії циркуляції (викликаної вихором) з плоскопаралельним потоком над обтічним тілом і під ним швидкості обтікання алгебраїчно складаються.

Рис. 63. Схема заміни циркуляційного обтікання приєднаним вихором

Таким чином, над профілем швидкість потоку збільшується, а під профілем – зменшується. Згідно з рівнянням Бернуллі, зміна швидкості обтікання призводить до зміни тиску над і під профілем, і в свою чергу викликає виникнення різниці тисків і, як наслідок, до появи підйомної сили.

Згідно з гіпотезою М. Є. Жуковського, навколо обтічного тіла виникає циркуляція швидкості, викликаної вихором, який Жуковський назвав приєднаним. Цей вихор викликає появу полів збурених швидкостей і тисків, які призводять до виникнення різниці тисків і, як наслідок, до утворення підйомної сили. Використавши теорему про імпульс сили, Жуковський встановив зв'язок між підйомною силою і циркуляцією швидкості.

Теорема про підйомну силу крила: якщо аеродинамічне тіло обтікаєтся сталим плоско-паралельним потоком нестисливої рідини, то на одиницю довжини цього тіла діє підйомна сила, яка прямо пропорційна масовій густині, швидкості потоку, циркуляції швидкості по замкнутому контуру і довжині контура, який охоплює вихор:

	У формулу циркуляції швидкості введемо деякі спрощення і заміни: довжину контуру замінимо хордою профілю введемо коефіцієнт пропорційності , тоді формула циркуляції швидкості буде мати вигляд:
, де: Сya – коефіцієнт пропорційності, що характеризує підйомну силу, викликаною циркуляцією; b – хорда профілю, м.

	Підставивши вираз циркуляції швидкості в вихідне рівняння підйомної сили, отримаємо вираз:
, де: – площа обтічної поверхні, м^2.

Таким чином: підйомна сила залежить від коефіцієнта підйомної сили (Суа), швидкісного напору і площі поверхні обтічного тіла (S).

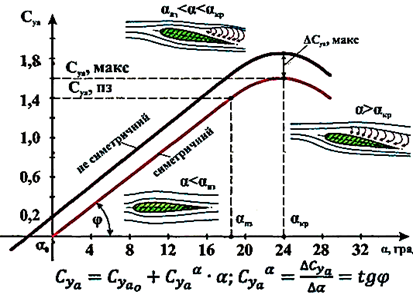
Коефіцієнт підйомної сили С_уа встановлює залежність підйомної сили від: положення обтічного тіла в потоці (від кута атаки 𝛼, форми профілю, структури потоку і форми тіла в плані. Коефіцієнт С_уа показує як ефективно використовується швидкісний напір при утворенні підйомної сили і характеризує несучі властивості профілю (рис. 64).

Характерні ділянки на графіку залежності :

– від до – обтікання плавне беззривне, залежність лінійна, прямо пропорційна зміні кута атаки;

– за досягнення через початок зриву з верхньої поверхні профілю порушується лінійність протікання графіка залежності ;

– за досягнення кута атаки величини критичного кута атаки коефіцієнт підйомної сили досягає максимального значення , зрив охоплює всю верхню поверхню профілю і подальше збільшення кута атаки призводить до зменшення коефіцієнта С_уа через зменшення перепаду тиску на профілі.

Задачі

1) Визначити циркуляцію швидкості і підйомну силу крила, якщо висота польоту Н = 1000 м, швидкість V = 480 км/год, коефіцієнт підйомної сили крила C_ya = 1,2, хорда крила b = 1,5 м, довжина контуру l = 10 м.

2) Визначити кут атаки (α₀), за якого коефіцієнт підйомної сили C_ya = 0, якщо коефіцієнт підйомної сили при куті атаки α = 5⁰ дорівнює C_ya = 0,8, похідна підйомної сили C_yα^a = 3, а також підйомну силу за швидкості V = 260 км/год і площі крила S = 40 м².

3) Визначити підйомну силу крила площею S = 100 м² для кута атаки α = 8⁰, якщо кут нахилу лінії графіка залежності C_ya = f (α) – φ = 30⁰, та коефіцієнт підйомної сили при куті атаки α₀ = мінус 2⁰, швидкість польоту V = 250 км/год.

Рис. 64. Графік залежності C_ya = f (α)

де:

– кут нахилу лінії графіка залежності С_уа = f ();

похідна графіка, що показує, як змінюється коефіцієнт підйомної сили за зміни кута атаки залежності С_уа = f ();

або

1.4.3. Фізична сутність газодинамічних особливостей і принцип моделювання потенційної течії

Витоком називається деяка газодинамічна особливість, яка формує потік рідини або газу, що витікає з деякого центру, званого джерелом, по радіусах сферичної поверхні з однаковою в усіх напрямках швидкістю (рис. 65).

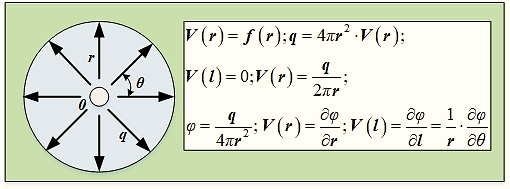
Об'ємна витрата рідини з джерела: .

Рис. 65. Схема газодинамічної особливості – витоку

	Тоді радіальна швидкість потоку рідини або газу дорівнюватиме:
Потенціал швидкості дорівнює: , де: – потенціал швидкості, який характирезує безвихровий потік (тобто потенційний, це – безвихрова течія).

За безвихрового руху рідини або газу швидкість залежить від координат, і це дає можливість визначити складові швидкості за координатами осей.

	Проєкції швидкості при плоскій течії в полярних координатах можна записати:

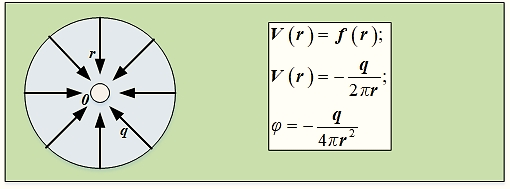
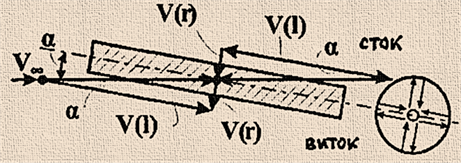
Наявність потенціалу швидкості дає можливість використовувати теорію безвихрових течій. Витік вводить в основний потік рідини або газу додатковий потік з деякою витратою рідини (q).

Стоком називається деяка газодинамічна особливість, яка формує негативний потік рідини або газу, що притікає з навколишнього простору до деякого центру по радіусах сферичної поверхні з однаковою для всіх напрямків швидкістю (рис. 66).

Рис. 66. Схема газодинамічної особливості – стоку

	Сток відбирає від основного потоку рідини або газу деяку частину рідини або газу з витратою (q). Швидкість радіального потоку стоку буде дорівнювати:
Для окремого випадку (плоскої течії) радіальні швидкості витоку і стоку можна розрахувати за формулою:

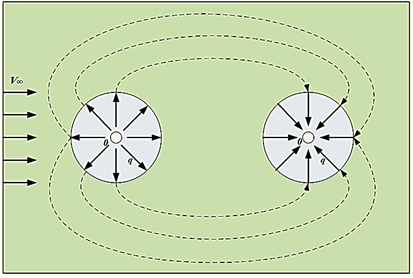
Для плоского випадку витрата має розмірність – м²/с, через площу поперечного перерізу.

Якщо зближувати між собою центри витоку і стоку, то утворюється новий вид газодинамічної особливості – диполь (дублет).

Диполем називається деяка газодинамічна особливість, утворена накладанням витоку і стоку на область, за якою формується потік рідини або газу з однаковими витратами (рис. 67).

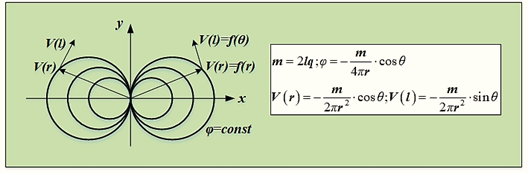
У цьому випадку відстань між джерелом і стоком прагне до нуля, а витрата – до нескінченності, зберігаючи при цьому момент диполя постійним.

	Момент диполя дорівнює:
, де: l – відстань між джерелом витоку і приймачем стоку, м; q – витрата рідини або газу, м^3/c. Потенціал швидкості дорівнює: , де: r – радіус-вектор диполя, м; 𝛉 – кут відхилення радіус-вектора від осі ОХ, радіани

Рис. 67. Схема формування газодинамічної особливості – диполя

Рис. 68. Схема виникнення газодинамічної особливості – диполя

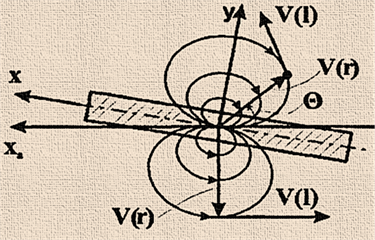
Нехай в _т.О знаходяться центр диполя, тоді лініями течії будуть окружності, центри яких лежать на осі ОX, загальна точка перетину кіл перебуває на осі ОХ.

	Окружні та радіальні швидкості диполя можна визначити за формулами:

Сутність моделювання несучих поверхонь за допомогою газодинамічних особливостей

Моделювання поля швидкостей, поля тисків і спектра обтікання за допомогою газодинамічних особливостей:

1. Вихровими шнурами (рис. 69):

Рис. 69. Схема моделювання несучих поверхонь

підковоподібним вихором

2. Витоками і стоками (рис. 70):

Рис. 70. Схема моделювання несучих поверхонь стоками і витоками

3. Диполями (рис. 71):

Рис. 71. Схема моделювання несучих поверхонь диполем

Питання для самоконтролю

1. Сутність вихрової течії рідини і газу, характеристика параметрів вихрової течії: напруга вихора, циркуляція швидкості, індуктивна швидкість. 2. Охарактеризувати формулу Біо-Савара для розрахунку індуктивної швидкості вихрового руху. Навести формули для розрахунку індуктивної швидкості для нескінченного і напівнескінченного вихорів. 3. Охарактеризувати сутність моделювання течії газового потоку і несучої поверхності ЛА прямолінійним вихором і його практичне використання. 4. Охарактеризувати теорему М. Є. Жуковського про підйомну силу крила: визначення, фізична сутність і розрахункова формула. 5. Охарактеризувати графік залежності коефіцієнта підйомної сили від кута атаки, його сутність і характерні ділянки на графіку залежності.

Попередня тема

На початок

Наступна тема