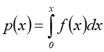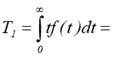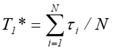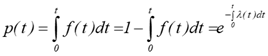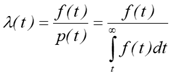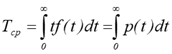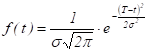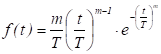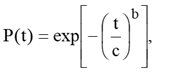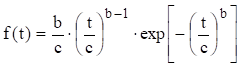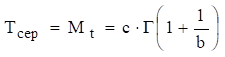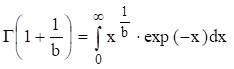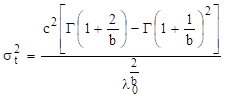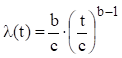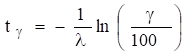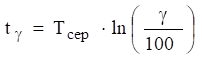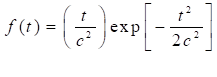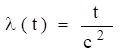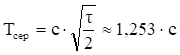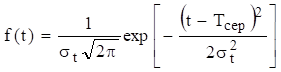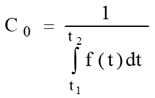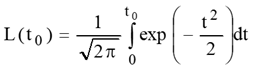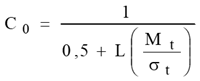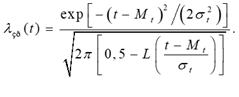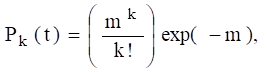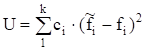|
|
|
Технічне обслуговування ремонт і монтаж машин
та агрегатів металургійних підприємств Частина I Електронний
посібник |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
РОЗДІЛ 1. НАДІЙНІСТЬ МАШИН |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1.4. Основи теорії надійності. 1.4.1. Наука про надійність. Термінологія, поняття, визначення, показники надійності 1.4.2. Фактори, що
впливають на надійність устаткування 1.4.3. Підхід до проєктування
і конструювання з позицій
теротехнології 1.4.4. Надійність елемента,
який працює до першої відмови 1.4.5. Методика обробки даних
статистичних спостережень
про надійність 1.4.6. Отримання інформації про надійність
обладнання 1.4.7. Елементи теорії ймовірності. Закони
розподілення напрацювання до відмов
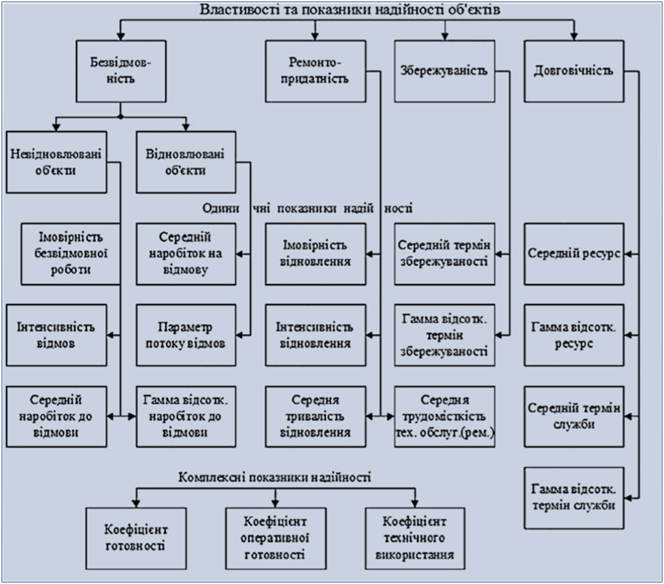
Надійність є
комплексною властивістю, яка, залежно від призначення об'єкта та умов його
застосування, може включати: ·
безвідмовність; ·
довговічність; ·
ремонтопридатність; ·
збережуваність або поєднання
цих властивостей. Безвідмовність – властивість
об'єкта безперервно зберігати працездатний стан протягом деякого часу або
напрацювання. Довговічність – властивість
об'єкта зберігати працездатний стан до настання граничного стану за
встановленої системи технічного обслуговування і ремонту. Ремонтопридатність – властивість
об'єкта, що полягає в пристосованості до підтримання і відновлення
працездатного стану шляхом технічного обслуговування і ремонту. Збережуваність – властивість об'єкта зберігати в заданих
межах значення параметрів, що характеризують здатність об'єкта виконувати
необхідні функції під час та після зберігання і транспортування.
Для опису різних пошкоджень
об'єктів використовують наступні терміни. Дефект – кожна невідповідність
властивостей об'єкта встановленим вимогам. Ушкодження – подія, що
полягає в порушенні справного стану об'єкта за збереження працездатного
стану. Відмова – подія, що
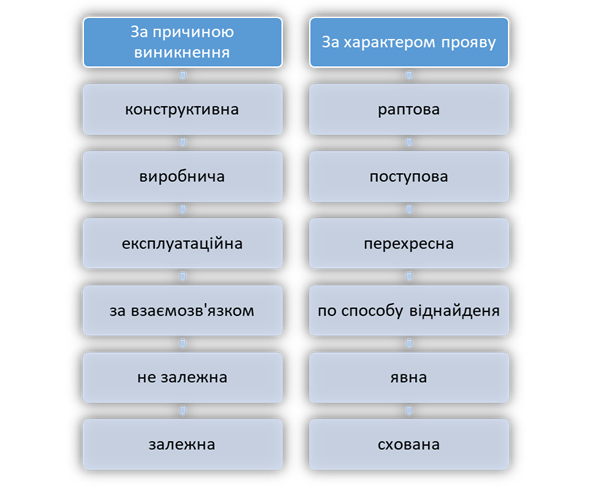
полягає в порушенні працездатного стану об'єкта. Розрізняють наступні типи відмов:
· ресурсна відмова,
в результаті якої об'єкт досягає граничного стану; · незалежна
відмова, що не обумовлюється іншими відмовами; · залежна відмова; · раптова відмова; · поступова
відмова; · збій – відмова,
що самоусувається, або одноразова відмова, що усувається незначним втручанням
оператора; · явна відмова
(виявляється візуально); · прихована
відмова; · конструктивна відмова; · виробнича
відмова; · експлуатаційна
відмова.
Надійність є комплексним показником якості машин, оскільки в нього
входять довговічність, збережуваність і ремонтопридатність.
Ремонтопридатність – показник тимчасовий. У технічно розвинених країнах він
відсутній, оскільки машини, які відпрацювали свій паспортний ресурс,
відправляють на металобрухт. Комплексним показником надійності є коефіцієнти готовності і технічного
використання. Коефіцієнт готовності – вірогідність того, що машина
буде працездатна в довільний момент часу в проміжках між плановими ремонтами,
окрім планованих періодів, в перебігу яких застосування машини не
передбачається. У сталому режимі експлуатації коефіцієнт готовності:
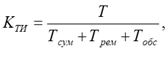
Коефіцієнт технічного використання – відношення інтервалів часу перебування
машини в працездатному стані на деякий період експлуатації до суми інтервалів
часу перебування машини в робочому стані, простоїв, обумовлених технічним
обслуговуванням і ремонтів за той же період експлуатації.
де: Тсум – сумарне напрацювання всіх
однакових об’єктів, експлуатованих в заданий період; Трем – сумарний час непрацювання
машини у зв’язку з плановими ремонтами; Тобс
– сумарний час непрацювання
машини у зв’язку з плановим і неплановим техничним обслуговуванням. Вірогідність безвідмовної роботи:
де n′ – число машин, які вийшли з ладу; n – число
машин, які безвідмовно пропрацювали до моменту часу; N – число випробованих машин. Для машин, які за системою ППР підлягають капітальним
ремонтам, велике зна- чення
має комплексний показник рівня ремонтопридатності. Під час аналізу надійності розраховується також решта характеристик експлуатаційної
надійності.
Для обгрунтованої оцінки надійності технічних пристроїв важливо правильно розуміти
природу та суть відмов.
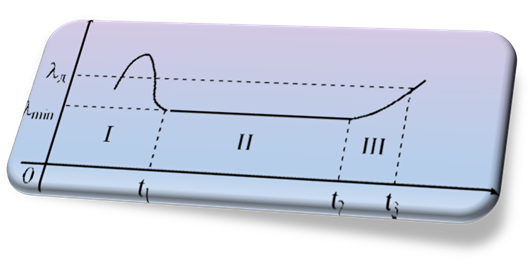
Під
час експлуатації розрізняють три типи відмов: відмови припрацювання, раптові та відмови внаслідок зносу. Вони відрізняються фізичною природою, способами
попередження та усунення і виявляються
в різні періоди експлуатації технічних пристроїв.
У житті машини можна виділити три основних періоди: проєктування, виготовлення та експлуатації.
Кожен із цих періодів
впливає на надійність, яка проявляться лише на останній стадії. Реальні деталі мають складну форму, яка
впливає на розподіл механічних навантажень. Тому при розрахунках форму
деталей спрощують. А це також веде до зниження точності розрахунків. З викладеного можна зробити висновок,
що дійсні механічні напруження практично неможливо передбачити, що впливає на
надійність виробу. Зважаючи на викладене, треба пам'ятати, що збільшення
коефіцієнтів запасу міцності не завжди призводить до зменшення напружень,
особливо у випадках динамічного навантаження (пуск, гальмування), оскільки за
зростання розмірів зростають і маси рухомих деталей. Крім того, збільшення
розмірів деталей призводить до збільшення їх вартості
та масштабного фактору.
Велике значення під час проєктування машини має вибір матеріалу деталей. Загалом, міцніші матеріали менш пластичні, в цих матеріалах більше
виникає тріщин, особливо за циклічних та ударних
навантажень. В той же час ці матеріали добре витримують контактні
навантаження під час статичних навантажень, зносостійкі. Матеріали з меншою
міцністю практично мають протилежні властивості, тому
використовуються в інших випадках. Але в практиці виникає потреба забезпечувати достатню міцність і здатність витримувати змінні навантаження.
В цих випадках використовують спеціальне термічне
або
інше оброблення. Останнім часом
широко використовують композитні матеріали, властивості яких
можна забезпечити під час їх виготовлення. Такими є матеріали на
основі високоміцних волокон. Під час проєктування машин та механізмів слід враховувати вплив різних конструктивних факторів, таких як проточки, галтелі, отвори, тобто таких конструктивних елементів, які зумовлюють зміну форми
деталі в межах невеликого обсягу. В таких місцях виникає нерівномірний розподіл механічних
напружень, який у техніці враховують
коефіцієнтом концентрації напружень. На значення коефіцієнта впливає не тільки зміна форми,
а й зміна характеру навантаження. Так, при посадках
втулок із натягом між втулкою та валом виникають нормальні напруження. Вони мають місце між валом та втулкою, але їх немає за межами втулки. Тобто на межі втулки буде мати місце різка зміна навантаження.
Це і призведе до появи концентрації напружень.
Водночас, для деталей машин, які працюють в умовах динамічного навантаження, фіксація взаємного розташування деталей без посадок із натягом майже
неможлива. З метою попередження поломок деталей машин
та механізмів на етапі проєктування
в машинах передбачають запобіжні пристрої. Пристрої можуть
мати руйнівний елемент. Запас міцності цих елементів близький
до одиниці. Внаслідок перевантаження ці деталі першими виходять із ладу і тим самим не дають можливості перевантажитись іншим деталям. Запобіжні деталі роблять
якомога простішими за формою та з не дуже
дорогого матеріалу. До таких деталей слід віднести втулки, стакани, зрізні болти, муфти, шпинделі тощо. В електричних схемах приводів передбачають тепловий та максимальний захист, які захищають
двигун від перевантаження та перегрівання. Кожне з перерахованих явищ не детерміноване, воно випадкове. Тому на надійність обладнання впливає велика
кількість випадкових факторів, які треба
враховувати на стадіях проєктування,
виготовлення та експлуатації машин
та механізмів.
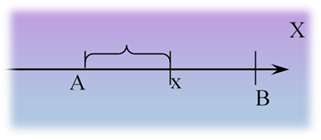
Якщо випадкова величина Х може
приймати будь-яке значення в деякому інтервалі [А, В], то для кожного
При цьому
Функція 1
–
Залежно від виду функції щільності
імовірності розділяють різні розподіли випадкових величин: рівномірне,
трикутне, експотенційне, нормальне, гама,
логарифмічно нормальне, Вейбула, Ст’юдента, Х2
(Хі - квадрат) та
інші. Основними числовими
характеристиками розподілів безперервних випадкових величин, які
використовуються в теорії надійності, є: Математичне очікування М(Х)
Дисперсія
Середньоквадратичне відхилення
Коефіцієнт варіації
Модель надійності. В момент Величина r може бути описана з допомогою
функції розподілу
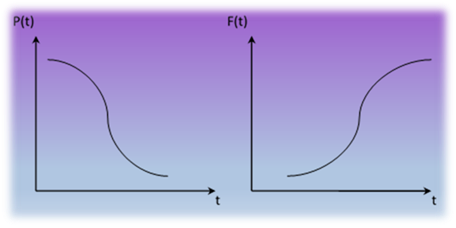
Функція Функція Поряд з функцією
Ця функція характеризує
імовірність без відповідної роботи. Цю функцію іноді називають функцією надійності. Статистична оцінка імовірності
безвідмовної роботи в межах напрацювання елемента від 0 до t, яка визначається згідно з даними
випробувань, має наступний вид
Статистична оцінка щільності
розподілу
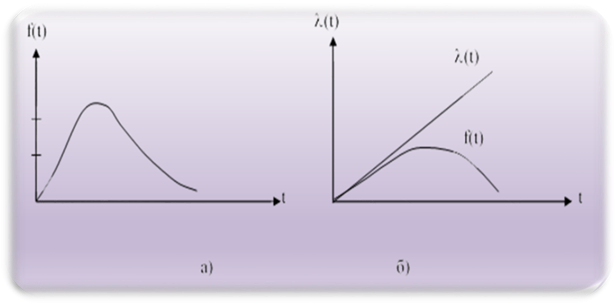
Графіки функцій
У більшості випадків на практиці
нема потреби характеризувати випадкову величину повністю. Досить буде
визначити тільки окремі числові характеристики. Найбільш важливою є середнє
напрацювання на відмову, яке визначається як математичне очікування величини
Статистична оцінка Т1 може бути виконана за
наступною формулою:
Другою важливою характеристикою
надійності виробів, які не демонтуються, є інтенсивність відмов.
Статистична оцінка інтенсивність
відмов
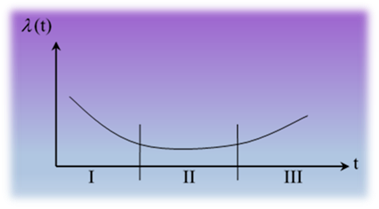
При випробуванні групи однотипних
має місце закономірність зміни
Між основними параметрами
надійності ·
щільність
імовірність відмов ·
імовірність
безвідмовної роботи ·
інтенсивність
відмов ·
напрацювання
до першої відмови (напрацювання на відмову) ·
математичне
очікування тривалості відновлення працездатності ·
коефіцієнт
готовності існують наступні математичні
залежності:
У теорії надійності в більшості
практичних випадків зустрічаються наступні функції щільності імовірності
відмов:
Визначення показників надійності
пов’язане з рішеням двох головних задач
математичної статистики – оцінка невідомих параметрів вибірки (множина
випадкових даних про напрацювання на відмову) та перевірки статистичних
гіпотез відносно законів розподілу ймовірності значень напрацювання на
відмову. Обробка результатів дослідження
надійності дозволяє вирахувати числові характеристики емпіричного розподілу
(вибірки) ймовірності значень напрацювання на відмову, які називаються
статистичними оцінками (емпіричними або вибірковими характеристиками), які
аналогічні числовим характеристикам ВВ (випадкової величини – величини
напрацювання на відмову): математичне очікування, дисперсія, початкові та
центральні моменти різних порядків. Кожній числовій характеристиці ВВ відповідає
її статистична аналогія. Математичним очікуванням
де
За необмеженого збільшення
Метою збирання
інформації про надійність обладнання є: отримання статичних даних, необхідних
для визначення кількісних значень показників надійності; встановлення
статистичних закономірностей відмов; визначення законів розподілення
випадкових значень часу безвідмовної роботи, відновлення, ресурсів щодо
капітального ремонту; виявлення елементів, що визначають вплив на рівень
надійності будь-яких гірничо-металургійних машин та систем обладнання в
цілому; вивчення впливу умов та особливостей експлуатації машин на рівень їх
надійності. На основі таких
даних можуть прийматися перевірені рішення щодо підвищення надійності машин,
комплексів, агрегатів та інших об’єктів промислового обладнання на стадіях проєктування, виготовлення та щодо підтримки необхідного
рівня їх надійності в процесі експлуатації. Для отримання
інформації щодо експлуатаційних властивостей використовують результати
спеціальних досліджень та документацій. Джерелом отримання досить повної
інформації про надійність обладнання та його елеменів
є Журнал спостережень за роботою обладнання, форма та вказівки щодо ведення
якого розроблені в галузевих нормативних матеріалах. Такий журнал
заповнюється силами обслуговуючого техніку персоналу, і є джерелом отриманя систематичної інформації про надійность
основних елементів серійного обладнання. Для визначення
показників елементів надійності, ліквідацій відмов, які виникли внаслідок
простоїв обладнання, можуть бути використані також журнал реєстрації відмов,
що ведеться механіком або диспетчерами виробництв. Найбільш повну
та різносторонню інформацію дають спеціальні хронометражні спостереження,
перевагами яких є безперервність та цільова спрямованість. Тривалість
спостережень залежить як від величини параметрів відмов обладнання (зі зменшенням якої вона
має зростати), так і від мети спостереження – потрібно визначити або
наскільки достовірне середнє значення показників надійності, або встановити
закон розподілу випадкових величин, які використовуються для оцінки
надійності. Під час
проведення певних випробовувань з метою
оперативного отримання кількісних значень показників надійності та параметрів
розподілу ВВ виникає потреба мати справу із вибіркою об’єктів з-поміж
генеральної сукупності – з усією сукупністю однорідних об’єктів обладнання
або з вибірковими сукупностями реалізації випадкових величин, які
використовують для оцінки надійності. Внаслідок цього, величина показників
надійності, визначена на основі вибіркової сукупності, лише з деякою
вірогідністю кількісно представляє ці показники для генеральної сукупності об’єктів.Тому при плануванні обсягу певних випробовувань задаються показники, що кількісно
характеризують достовірність результатів (достовірна вирогідність)
та їх точність (зазвичай межа помилки).
Час
безвідмовної роботи –
випадкова величина. Найбільш повною її характеристикою є закон розподілу. В
теорії надійності використовується низка законів: Вейбулла-Гнеденко,
експоненціальний, Релея, Пуассона, нормальний, рівномірний та ін. Розподіл Вейбулла-Гнеденко використовується зазвичайно для опису показників надійності
напівпровідникових приладів, мікросхем і РЕП. Для цього розподілу ймовірність
безвідмовної роботи в інтервалі
де
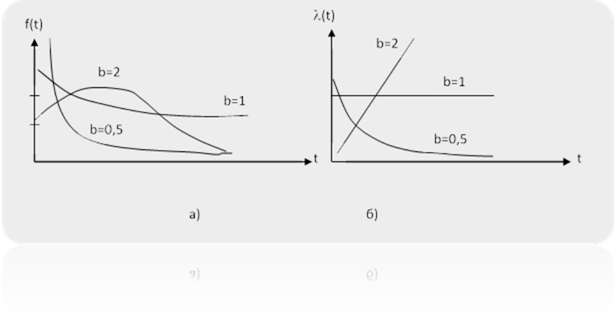
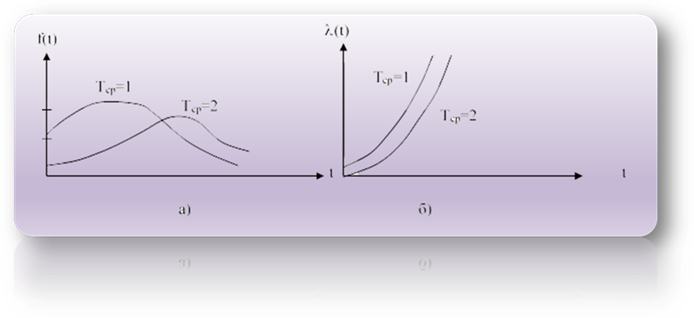
Щільність
ймовірності відмов (рис.1.66,а) дорівнює
середнє напрацювання до відмови
де Дисперсія середнього напрацювання
до відмови при цьому складає
Із формул (1.26) і (1.27)
Неважко визначити, що за Розподіл Вейбулла
за Отже,
ймовірність безвідмовної роботи
Щільність ймовірності
відмов
Середнє
напрацювання до відмови
Підстановка (1.30) в (1.32) дає
За експоненціальним розподілом
математичне сподівання випадкової величини дорівнює середньому квадратичному
відхиленню
Експоненціальний розподіл є типовим
для більшості складних РЕП, що складаються з великої кількості різноманітних
елементів, що не ремонтуються, які мають переважно раптові відмови. З
урахуванням (3.1) і (3.6)
Отже
З урахуванням (1.34)
Графіки щільності ймовірності
відмов Розподіл Релея досить повно описує поведінку РЕП і їх елементів з явно
вираженим ефектом старіння і зношеності. Ймовірність
безвідмовної роботи
Щільність ймовірності відмов
(рис.1.2, а)
Інтенсивність
відмов (рис. 1.67, б)
Середнє напрацювання до відмови
Середнє квадратичне відхилення
середнього напрацювання до відмови
Тут – параметр розподілу.
Нормальний розподіл описує надійність об’єкта, для
якого характерне зношування однорідних елементів, які мають малий розкид
параметрів зношуваності. Щільність ймовірності відмов
За нормального розподілу випадкова
величина може мати будь-які значення від – Для зрізано нормального на
інтервалі
При цьому, якщо
Тоді
де Для зрізаного розподілу
ймовірність безвідмовної роботи
Далі всі параметри, які
характеризують зрізаний розподіл, будуть мати індекс “зр”. Значення функції Лапласа табульовано тільки для додатних аргументів. У випадку
від’ємних значень аргументів застосовують правило: Диференціальна
функція зрізаного розподілу (рис. 1.67, а)
Середнє
напрацювання на відмову
Середнє
квадратичне відхилення нормального зрізаного розподілу
Інтенсивність відмов нормального
зрізаного розподілу (рис. 1.68, б)
Рівномірний розподіл використовується для оцінювання
надійності об’єктів щодо повторюваних відмов для деякого інтервалу часу Ймовірність
безвідмовної роботи
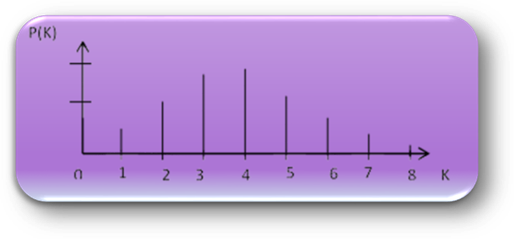
Розподіл Пуассона (рис. 1.69) описує поведінку
дискретних випадкових величин. Випадкова величина
де
Дисперсія випадкової величини
Інтенсивність відмов дорівнює
Оскільки функція Визначення закону
розподілу Для розрахунку показників
надійності за статистичними даними необхідно визначити закон розподілу
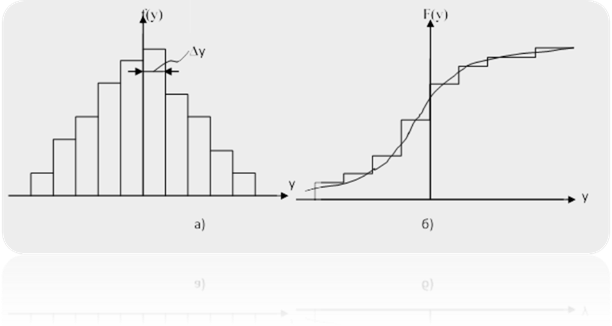
випадкового часу напрацювання на відмову. Для цього вибірку даних N поділяють на L інтервалів за формулою:
Після цього визначають частоту
попадань значень випадкової величини напрацювання на відмову в кожний
інтервал
де Побудувавши графік частоти
попадань
Критерій Пірсона застосовують для вибірки від 50 до
100 результатів Він передбачає використання
з вагами Критерій Колмогорова (для вибірки більш 100
результатів) як міру розбіжності теоретичного
й експериментального розподілів використовує максимальне значення модуля
різниці D між експериментальною
Колмогоров довів, що якою б не була функція розподілу випадкової величини, за
необмеженого зростання числа незалежних спостережень ймовірність нерівності
В критеріях Пірсона і Колмогорова величину Прийнято
вважати, що теоретичний розподіл не суперечить експериментальним даним, якщо На практиці при застосуванні
критерію Пірсона розраховують міру відхилення одержаного
закону від теоретичного:
де
За повної відповідності емпіричної
та теоретичної вибіркових частот Для оцінювання відповідності
емпіричного розподілу теоретичному необхідно розрахувати фактичне значення Наприклад, для
побудови теоретичної кривої нормального розподілу достатньо два параметри –
математичне сподівання та середнє квадратичне відхилення, тому
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||