ОСНОВИ АЕРОДИНАМІКИ ТА ДИНАМІКИ ПОЛЬОТУ

частина І

АЕРОГІДРОГАЗОДИНАМІКА

Електронний посібник

ГОЛОВНА	ТЕОРЕТИЧНІ ВІДОМОСТІ	АНОТАЦІЯ
ДОДАТКИ	СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

2. АЕРОДИНАМІЧНІ ХАРАКТЕРИСТИКИ ПРОФІЛЮ КРИЛА І НЕСУЧОГО ГВИНТА ВЕРТОЛЬОТА.

АЕРОДИНАМІКА ГІПЕРЗВУКОВИХ ПОТОКІВ І РОЗРІДЖЕНИХ ГАЗІВ

2.3. Особливості аеродинаміки гіперзвукових потоків і в розріджених газах

2.3.1. Особливості гіперзвукового обтікання тіл

2.3.2. Аеродинаміка тіл при обтіканні розрідженим газом

2.3.1. Особливості гіперзвукового обтікання тіл

Поняття про гіперзвукову течію

Польоти літаків при числах Маха M > 4 умовно вважаються гіперзвуковими.

Теорія гіперзвукових течій пов'язана з деякими особливостями обтікання твердих тіл в порівнянні з малими надзвуковими швидкостями:

- аеродинамічними, так як вони викликані необхідністю врахування у великій мірі стисливості через великі значення чисел Маха;

- фізико-хімічними, так як газовий потік при гіперзвукових швидкостях володіє високими енергетичними можливостями

1. Аеродинамічні ефекти в одних випадках дозволяють застосовувати спрощене рішення аеродинамічних задач, пов'язаних з взаємодією ЛА з газовим потоком при великих гіперзвукових швидкостях, в інших випадках до значного їх ускладнення, так як метод лінеаризації диференціальних рівнянь руху, які застосовуються при моделюванні великих надзвукових течій, не застосовують для гіперзвукових течій.

2. Фізико-хімічні ефекти в гіперзвуковому потоці пов'язані з утворенням зон з високими температурами. Як правило вони виникають при переході гіперзвукового газового потоку через скачки ущільнення, на яких кінетична енергія руху перетворюється в теплову. При цьому високі температури змінюють фізичні властивості газового середовища: наприклад, при температурі Т = 2500⁰К і помірних тисках починається дисоціація молекул кисню; при температурі Т = 4000⁰К відбувається дисоціація молекул азоту; при температурі Т = 7000⁰К відбувається іонізація атомів азоту і кисню, при подальшому збільшенні температури відбувається іонізація молекул азоту.

Питомі теплоємності при таких високих температурах стають не постійними величинами і не залежать від температури. Тому в дослідженнях не застосовуються питомі теплоємності які отримані при постійних обсязі і тиску.

При гіперзвукових швидкостях неминучий сильний аеродинамічний нагрів поверхні обтікаємого тіла. Тому максимальна швидкість обмежується не тільки з умов отримання максимальної підйомної сили, а й з умов максимально-допустимого кінетичного нагріву обшивки ЛА.

Особливостями гіперзвукових течій є:

1. Зі збільшенням числа Маха (↑ M) зменшується кут нахилу скачка ущільнення, при цьому він наближаються до поверхні обтікаємого тіла, зменшуються області збурень між стрибком і тілом. Це призводить до взаємодії стрибка і примежового шару. Головний стрибок обмежує збільшення примежового шару. Це призводить до збільшення темпеатури (↑ T) і зменшення масової густини (↓ ρ) і як наслідок до збільшення товщини примежового шару (↑ δ). При цьому створюється ефект збільшення товщини обтікаємого тіла, що призводить до викривлення ударної хвилі і збільшення тиску (↑ p).

2. Малі зміни параметрів руху обтікаємого тіла призводять до суттєвих змін параметрів газу. При M >> a, збурені швидкості течії можуть бути одного порядку зі швидкістю звуку.

3. Із-за високих температур за головною хвилею і в примежовому шарі можуть мати місце дисоціація і іонізація газу, що призводить до зміни його термодинамічних властивостей.

Таким чином, при гіперзвукових течіях методи дослідження аеродинамічних характеристик, які застосовуються при дозвукових і помірних надзвукових швидкостях течії газу, стають непридатними.

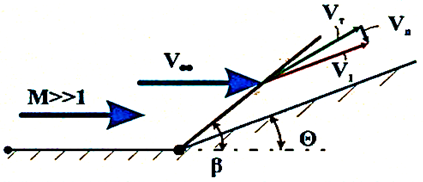
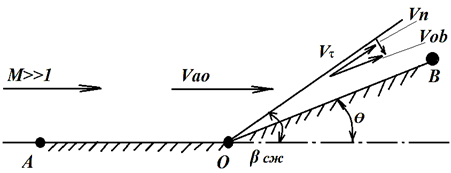
При розгляді обтікання тіл під невеликим кутом атаки рівняння руху можна спростити і отримати алгоритми наближеного визначення аеродинамічних характеристик ЛА при гіперзвукових швидкостях польоту.

Стиснення потоку проходить на стрибку ущільнення ОС (рис. 223):

При збільшенні надзвукової швидкості зменшується кут нахилу стрибка ущільнення до поверхні обтічного тіла (↑ М → β → ω)

;

Рис. 223. Схема виникнення стрибка ущільнення

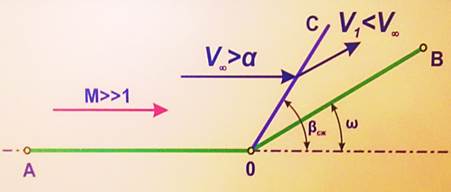
При обтіканні надзвуковим повітряним потоком зовнішнього тупого кута в точці зламу кута _т.О виникають сильні збурення у вигляді характеристик розширення.

Рис. 224. Схема виникнення характеристик розширення

При течії з розширенням надзвукового потоку поворот і його розгін відбувається на серії характеристик розширення ОС – ОС₁.

;

При збільшенні швидкості надзвукового потоку, кути нахилу стрибків і характеристик розширення мають кінцеві величини:

(↑ М → ∞, β_сж =ω; β_р = 0)

В цьому випадку, коефіцієнт тиску можна визначити за значеннями кута нахилу стрибка ущільнення і характеристики розширення за формулою:

р = 2 β ω;

Відносна зміна тиску, викликане зміною кута нахилу поверхні обтікаємого тіла можна визначити за формулою:

;

Особливості визначення аеродинамічних характеристик профілю крила при гіперзвукових швидкостях потоку.

Для наближеного розрахунку розподілу тиску по поверхні твердого тіла при гіперзвуковому обтіканні використовується гіпотеза І. Ньютона про корпускулярну теорію гідродинамічного опору. Відповідно до цієї теорії частинки набігаючого повітряного потоку залишаються незбуреними до зіткнення з поверхнею твердого обтікаємого тіла. При ударі частки втрачають нормальну складову своєї кількості руху і далі рухаються по дотичній до поверхні тіла.

	Нормальна ж складова кількості руху створює імпульс сили тиску, який діє на поверхню обтікаємого тіла (рис. 225):
р – p∞ = ρ∞ V∞^2 Sin^2Ɵ; де: Ɵ – кут між дотичною до поверхні обтічного тіла і вектором швидкості потоку, що набігає, рад.

Таким чином, через одиницю площі, паралельної похилій площині обтікаємого тіла за одиницю часу проходить цілком певна маса повітря:

m =ρ_∞ V_∞ Sin Ɵ;

Рис. 225. Схема обтікання внутрішнього кута гіперзвуковим потоком

	Коефіцієнт відносного тиску можна визначити за формулою:
; де: – зміна відносного тиску.

Тоді для тонких тіл, коли кут нахилу стрибка дорівнює куту нахилу поверхні обтікаємого тіла β = Ɵ, відносний тиск дорівнюватиме:

p = 2 Ɵ² _;

Застосування цієї формули при гіперзвуковому обтіканні обумовлена тим, що головна ударна хвиля досягає поверхні обтікаємого тіла.

Розрахунок сили тиску за формулою І. Ньютона досить точно описує гіперзвукову течію навколо тіла в граничних умовах: k = Cp/Cw = 1 і М∞ = ∞.

Для цього випадку коефіцієнт тиску в критичній точці гальмування вважається рівним: p_макс= 2.

В ході експериментів встановлено, що при k = 1,33 і М∞ = 15, p_макс= 1,75

	З огляду на те, що в загальному випадку стрибок ущільнення не суміщається з поверхнею обтікаємого тіла, то формула розрахунку тиску має вигляд:
p = pмакс Sin^2Ɵ; де: pмакс – тиск в критичній точці обтікаємого тіла, Па.

Тому розрахункову формулу можна перетворити:

;

Враховуючи що , а , отримаємо формулу для розрахунку тиску по поверхні обтікаємого тіла у вигляді:

p = p_∞ (1 + k M_∞² Sin²Ɵ);

Відповідно до теорії І. Ньютона тиск на елементарну площадку обтікаємого тіла залежить від положення цієї площадки відносно набігаючого потоку і не залежить від форми іншої частини тіла. Тому опір тіла визначається тільки формою його головної частини, так як тільки вона стикається з частинками набігаючого потоку. Тиск за корвомою частиною обтікаємого тіла дорівнює нулю.

З розглянутого можна зробити висновок, що в гіперзвуковому потоці коефіцієнт тиску за стрибком ущільнення, при малих кутах повороту потоку Ɵ, пропорційний Ɵ². Аналогічним чином можна визначити інші фізичні параметри газу за косим стрибком ущільнення при гіперзвукових швидкостях течії.

Так при куті атаки α = 0, коефіцієнт хвильового опору буде дорівнює:

С_ха,в =2 Sin²β;

Для отримання сумарного коефіцієнта опору, необхідно скласти коефіцієнти хвильового опору і опору тертя:

C_xa,_Σ = C_xa,_тр + C_xa,_в ;

Особливості виникнення стрибків ущільнення при гіперзвуковому обтіканні

З огляду на, що при гіперзвукових швидкостях течії стрибок ущільнення наближається до поверхні обтікаємого тіла, то потік повертається на невелику величину, тому можна вважати, що, = 1, тоді після перетворення рух гіперзвукового потоку через стрибок ущільнення матиме вигляд (рис. 226).

Рис. 226. Схема утворення стрибків ущільнення при гіперзвуковій течії

(M₁ β)² - (M₁ β) _* (M₁ Θ) - 1 = 0

Величини M₁ β і M₁ Θ називаються параметрами гіперзвукового подібності, їх можна замінити коефіцієнтами подібності:

K_α = M₁ Θ і K_c = M₁ β;

Підставивши їх у вихідне рівняння, отримаємо квадратичне рівняння:

K_c² - K_c K_α - 1 = 0;

Розвязавши це рівняння отримаємо корні параметрів гіперзвукової подібності:

K_c = K_α +

При малих значеннях кутів нахилу стрибка ущільнення β, отримаємо рівняння:

K_c²- звідси

p =;

Після перетворення, за умови, що M₁ → ∞, (K_α → ∞), отримаємо рівняння:

p = () Θ²;

Звідси можна зробити висновок, що в гіперзвуковому потоці коефіцієнт тиску за стрибком ущільнення при малих кутах повороту обтікаємих поверхонь Θ, пропорційний значеннюΘ². Аналогічним чином можна звизначити інші параметри газу за косим стрибком ущільнення при гіперзвукових швидкостях.

Поняття про аеродинамічне нагрівання конструкцій ПС і способи зниження нагрівання.

При польоті з великими надзвуковими швидкостями частина кінетичної енергії літака переходить в теплову, що може привести до підвищення температури обшивки літака. Аеродинамічне нагрівання поверхні літака в значній мірі обмежує можливості швидкісних літаків, перешкоджаючи підвищенню швидкості польоту. Аеродинамічний нагрів обшивки літака починає інтенсивно проявлятися при швидкості польоту М > 2. Для забезпечення необхідного запасу міцності обшивки при аеродинамічному нагріванні доводиться збільшувати вагу літака, ускладнювати конструкцію, що погіршує аеродинамічні характеристики літаків.

Аеродинамічний нагрів створює так званий «тепловий бар'єр», який виникає при досягненні швидкості польоту М > 3 і ставати надзвичайно небезпечним при М > 4.

При польоті літака з гіперзвуковими швидкостями в примежовому шарі відбувається не тільки збільшення швидкості, але і температури. Найбільша температура виникає в місці гальмування потоку в критичній точці теоретично до «0». Внаслідок відведення тепла теплопровідністю з пристіночної області примежового шару в зовнішні області шару, температура поблизу поверхні обшивки менше температури гальмування.

	При відсутності теплообміну примежового шару з поверхнею обшивки температура повітря біля поверхні дорівнює температурі гальмування і називається температурою відновлення:
Tr = Т∞ (1 + r M∞^2); де: r – коефіцієнт відновлення температури.

Величина коефіцієнта відновлення (r) практично не залежить від чисел М і Re, але залежить від характеру розподілу швидкостей по перерізу примежового шару і швидкістю відводу тепла теплопровідністю з пристіночної області примежового шару.

	Відношення відведення тепла теплопровідністю до виділення тепла за рахунок тертя в примежовому шарі характеризується числом Прандтля:
Pr=; де: μ – коефіцієнт динамічної в'язкості повітря; Ср – питома теплоємність при р = const; λ – теплопровідність повітря.

Коефіцієнт відновлення температури (r) залежить від структури примежового шару:

- для ламінарного шару r = 0,85;

- для турбулентного шару r = 0,9.

Зі збільшенням висоти польоту ступінь нагріву зменшується внаслідок зменшення масової густини повітря.

При нагріванні, внаслідок, великих перепадів температури в елементах конструкції виникають додаткові напруги і з'являється повзучість матеріалу конструкції, що зменшує запас міцності обшивки.

Передача тепла всередину обшивки літака при польоті з гіперзвукової швидкістю (М > 4) і вище ускладнює роботу екіпажу і призводить до підвищеної випаровуваності палива з паливних баків літака.

Процес передачі теплової енергії від рухомого нагрітого повітря до твердого тіла називається конвективним теплообміном. Нагріта обшивка літака випромінює в навколишнє середовище певну кількість енергії у вигляді електромагнітних хвиль, в основному в інфрачервоній частині спектра. Крім конвективного теплового потоку в теплообміні присутній тепловий потік, викликаний сонячною радіацією, а також джерелами тепла, що знаходяться всередині обшивки літака.

Все кількість тепла, яке досягає поверхні обшивки літака як із зовні, так і з середини літака, витрачається на підвищення температури конструкції літака.

Таким чином, виникає тепловий баланс: кількість підведеного до обшивки літака тепла від усіх джерел дорівнює кількості відведеного тепла:

q_конв + q_солн ± q_обш - q_ізл = 0

	Питомий конвективний тепловий потік визначається за формулою:
qконв = α (Tr - Tw); де: Tw – рівноважна температура між середовищем і тілом; Tr – температура відновлення; α – коефіцієнт теплопередачі між середовищем і поверхнею тіла.

	Питомий тепловий потік від випромінювання обшивки літака визначається за формулою:
qізл = σ ε Tw; де: ε – коефіцієнт чорноти поверхні тіла; σ – теплова постійна Стефана-Больцмана.

	Питомий тепловий потік від сонячної радіації визначається за формулою:
qсолн = As βs Gs ; де: φ – кут нахилу поверхні тіла до сонячних променів; As – коефіцієнт затінення поверхні, що враховує стан атмосфери, наявності хмарності; βs – коефіцієнт поглинальної здатності поверхні тіла; Gs – кількість сонячної енергії, що підводиться до 1м^2 площі тіла в секунду.

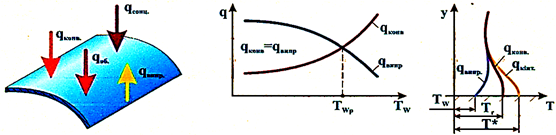
Розвязування рівняння теплового балансу зазвичай здійснюється графічним методом. Згідно результатів досліджень теплового балансу температура поверхні тіла (T_w) значно вище температури незбуреного середовища (рис. 227).

Перехрещення кривих конвективного теплового потоку і теплового потоку випромінювання дозволяє визначити температуру рівноважного стану T_w:

q_конв = q_ізл

Рис. 227. Графік залежності теплового потоку від температури рівноваги

Для зниження аеродинамічного кінетичного нагріву обшивки літака при великих числах Маха необхідно зменшувати коефіцієнт тепловіддачі (α) і збільшувати ступінь чорноти (ε).

Заходи зниження коефіцієнта тепловіддачі (α):

- збільшення висоти польоту, призводить до зменшення масової густини повітря;

- ламінірізація примежового шару, що дозволяє зменшити швидкість течії біля поверхні тіла за рахунок утворення ентропійного шару.

- заходи збільшення випромінювальної здатності поверхні тіла (ε):

- виготовлення елементів конструкції обшивки літака з матеріалів які мають високе значення коефіцієнта чорноти (ε).

Задача

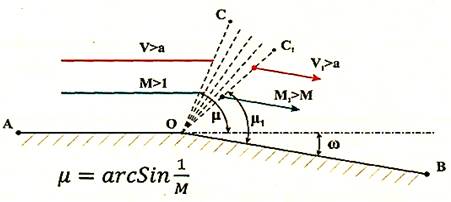
Визначити кут нахилу стрибка ущільнення і коефіцієнт тиску, якщо повітряний потік набігає на профіль з швідкітю 2000 км/год на висоті 1000 м, поверхня сторони внутрішнього кута нахилена на кут 5⁰.

2.3.2. Аеродинаміка тіл при обтіканні розрідженим газом

Особливості аеродинаміки тіл в розріджених газах

В умовах розрідженого газу необхідно враховувати його молекулярну структуру, яка виражається довжиною вільного пробігу молекул від одного зіткнення до іншого.

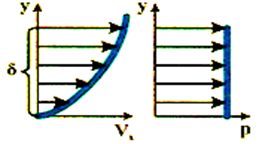
У зв'язку з тим, що швидкості хаотичного руху окремих молекул можуть змінюватися в широких межах, довжина вільного пробігу різних молекул не однакова. Тому основним параметром течії розрідженого газу є середня довжина вільного пробігу молекули.

Розглянемо епюру швидкостей з просковзуванням відповідно до теорії Кнудсена про суцільність середовища і простежимо взаємодія двох сусідніх шарів газу в примежовому шарі, що знаходяться один від одного на відстані, рівному довжині вільного пробігу молекули (l) (рис. 228).

Рис. 228. Графік епюри швидкостей і тиску в примежовому шарі

В силу хаотичного руху молекули переміщаються з одного шару в інший і навпаки.

	Маси молекул перетікають через одиничну площадь шару за одиницю часу буде пропорційна середній швидкості хаотичного руху молекул і масовій густині газу:
m = k1 ρ V; де: k1 – коефіцієнт пропорційності; ρ – масова щільність, кг/м^3; V – середня швидкість хаотичного руху молекул, м/с.

Зміна кількості руху газу при хаотичному русі визначається по формулі:

m = k₁ ρ V;

Імпульс сили тертя за одиницю часу можна визначити за формулою Ньютона:

τ = μ

З фізики відомо, що імпульс сили дорівнює зміні кількості руху маси рухомого газу:

μ =k₁ ρ V;

Звідси можна отримати середню довжину вільного пробігу молекул:

	Середню швидкість вільного пробігу молекул можна визначити використовуючи молекулярно-кінетичну теорію газу:
V = a; де: a – швидкість звуку, м/с; k – показник адіабати;

З огляду на це, формула середньої довжини вільного пробігу молекул матиме вигляд:

;

Зі збільшенням висоти атмосфери довжина вільного пробігу молекул сильно змінюється: так у землі l – це мільйонні частки сантиметра; на висоті 120 км - l – кілька метрів; на висоті 200 км - l – сотні метрів.

Якщо відношення довжина вільного пробігу молекул до товщини примежового шару більше 1 (), То така область називається областю вільно молекулярної течії. У цій області елементарні частинки не взаємодіють між собою і примежового шару фактично немає. Сили взаємодії між потоком і тілом представляють собою імпульс сили ударів частинок повітря об поверхню тіла.

Так як товщина примежового шару залежить від характеру течії та числа Re, то отже число Кнудсена K_nδ також буде залежати від чисел Рейнольдса і Маха.

≈ , тоді K_nδ≈ ;

При малих числах Рейнольдса Re число Кнудсена – K_nδ ≈

Таким чином, В залежності від числа Re вводиться критерій розрідженості середовища:

або .

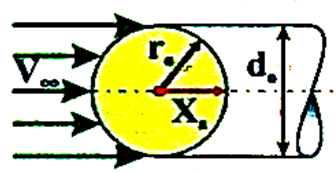
Підйомна сила і сила лобового опору в молекулярному потоці розрідженого газу

У вільно молекулярному потоці единими силами впливу газового середовища на рухоме в ній тіло є сили зіткнень молекул газу об поверхню тіла.

Ці сили можна визначити, якщо відомий закон руху молекул після удару об поверхню тіла.

Існує кілька схем відскакування молекул після удару від поверхні тіла, але найбільш близькими до реальних умов є схеми (рис. 229):

- дзеркального відскакування;

- дифузійного відскакування

Рис. 229. Схеми відскакування молекул від поверхні твердих тіл

1. При дзеркальному відскакувані молекули після зіткнення з тілом відскакують від нього під таким же кутом, під яким вони взаємодіяли з тілом.

2. При дифузійному відскакувані молекули відскакують від тіла під різними кутами, так як поверхні тіл не є ідеально рівними. В цьому випадку молекули газу, вдаряючись об поверхню тіла, віддають йому всю свою кінетичну енергію, потім на деякий час як би прилипають до поверхні тіла і поглинаються нею. За цей час відбувається вирівнювання температури газу і поверхні тіла. Після чого молекули відскакують від тіла під відповідним кутом зі швидкістю, що відповідає температурі поверхні тіла. Величину аеродинамічних сил, що діють на тіло в вільно молекулярному потоці можна оцінити по ударній (корпускулярній теорії) теорії І. Ньютона.

У цій теорії використовується ще одна схема відскакування молекул – схема непружного відбиття. Відповідно до цієї теорії частинки газу при ударі повністю втрачають швидкість і як би прилипають до тіла (рис. 230).

Рис. 230. Схема впливу рухомих молекул на сферичні тіла

У цьому випадку дії вільно молекулярного потоку піддається лише передня частина поверхні сфери. Сила опору кулі буде дорівнювати сумарному імпульсу від сили ударів молекул при зміні кількості руху маси молекул газу об передню частину поверхні сфери.

	Масу молекул, що вдаряються об поверхню тіла, можна визначити:
m = ρ∞ V∞ S де: S = π r0^2 – площа миделевого перерізу сфери, м^2; V∞ – середня швидкість вільного руху молекул, м/c.

Згідно теореми про зміну кількості руху при зіткненні молекул з тілом виникає імпульс сили, який передається на кулю у вигляді сили лобового опору.

m V_∞ = ρ_∞ V_∞² S = Х_а ;

Якщо розділити це рівняння на швидкісний натиск і на площу міделевого перерізу то отримаємо коефіцієнт лобового опору в вільно молекулярному потоці:

С_xа = = 2;

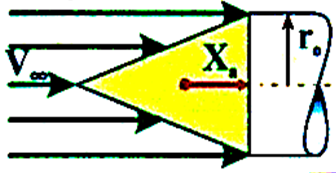
Аналогічний результат як у випадку обтікання кулі, можна отримати і в разі обтікання конуса, якщо прийняти, що на поверхні конуса частинки газу повністю загальмовуються (рис. 231):

Рис. 231. Схема обтікання потоком молекул конуса обертання

Х_а = ρ_∞ V_∞² S;

;

де:

S – площа міделевого перерізу конуса, м²

Силу лобового опору і її коефіцієнт плоскої пластини можна визначити використовуючи теорему про кількість руху маси газу обтікаємого пластину (рис. 232):

Рис. 232. Схема обтікання потоком молекул плоскої пластини

Х_а = m V_∞ = ρ_∞ V_∞² S = ρ_∞ V_∞² b l Sin α; С_Ха = 2 Sin α;

Таким чином, ударна теорія І. Ньютона показує, що єдиною аеродинамічною силою при русі тіла в розрідженому середовищі є сила лобового опору.

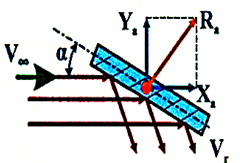
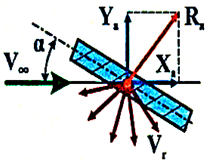
Так як в реальних умовах майже 97% молекул відбиваються від поверхні тіла диффузійно, то отже, молекули при відскакуванні від тіла віддають додаткову, нормальну до поверхні пластини, силу, аналогічно підйомній силі. Тому в вільно молекулярному потоці на пластині будет виникати невелика за величиною підйомна сила, а сила лобового опору буде значно більшою за величиною, ніж сила опору, що визначається відповідно до теорії Ньютона.

При дифузійному відскакувані коефіцієнти аеродинамічних сил і моментів, що діють на тіла різної форми визначаються на основі молекулярно-кінетичної теорії газів. Відповідно до теорії в разі дифузійного відскакування молекул коефіцієнти С_xаі С_уа плоскої пластини залежать від числа Маха (М), кута атаки (α) і відношення найбільш ймовірних швидкостей теплового руху відображених молекул (V_r) до швидкості вільних молекул (V_∞):

Отже, для визначення коефіцієнтів С_{xа і} С_уа плоскої пластини в вільномолекулярном потоці газу необхідно знати температуру відбитого потоку молекул газового потоку і температуру відновлення (T_r).

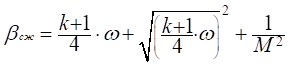
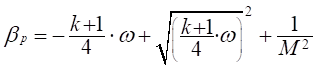
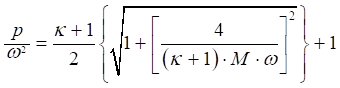
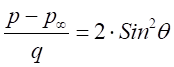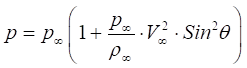
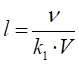
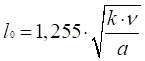Питання для самоконтролю

1. Поняття про гіперзвукову течію. 2. Аеродинамічні характеристики тіл при гіперзвуковому обтіканні. 3. Особливості виникнення стрибків ущільнення при гіперзвукових швидкостях. 4. Аеродинамічні характеристики профілів при гіперзвукових швидкостях обтікання. 5. Поняття про аеродинамічне нагрівання конструкцій ПС. 6. Способи зниження нагрівання поверхні ПС. 7. Особливості аеродинаміки розріджених газів. 8. Підйомна сила і сила лобового опору в молекулярному потоці розрідженого газу. 9. Особливості розрахунку аеродинамічних сил і моментів при гіперзвуковому обтіканні. 10. Особливості розрахунку аеродинамічних сил і моментів при обтіканні розрідженим газом.

Попередня тема

На початок