МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

ПАРАЛЕЛЕПІПЕД

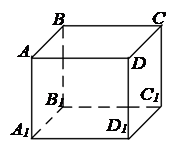
Паралелепіпед

Паралелепіпедом називають призму, основою якої є паралелограм (ABCD, A₁B₁C₁D₁).

У паралелепіпеда всі грані паралелограми: A₁ABB₁, B₁BCC₁, C₁CDD₁, D₁DAA₁.

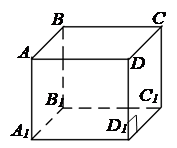
Паралелепіпед, бічні ребра якого перпендикулярні до площини основи, називають прямим паралелепіпедом. Його бічні грані – прямокутники.

Розглянемо властивості паралелепіпеда:

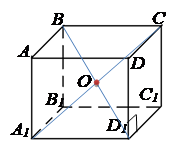
Теорема 1 (властивість протилежних граней паралелепіпеда). Протилежні грані паралелепіпеда паралельні та рівні.

Теорема 2 (властивість діагоналей паралелепіпеда). Діагоналі паралелепіпеда перетинаються і точкою перетину діляться навпіл (ВО=OD₁, CO=OA₁).

Прямокутний паралелепіпед

Прямокутним паралелепіпедом називають прямий паралелепіпед, основою якого є прямокутник.

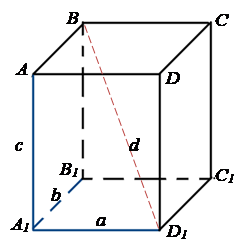
Всі грані прямокутного паралелепіпеда є прямокутниками, усі двогранні кути – прямими.

Довжини трьох ребер прямокутного паралелепіпеда, які виходять з однієї вершини, називають вимірами (або лінійними вимірами) прямокутного паралелепіпеда.

Теорема 3 (формула для обчислення довжини діагоналі прямокутного паралелепіпеда). Квадрат діагоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів.

Наслідок. Усі чотири діагоналі прямокутного паралелепіпеда рівні.

Прямокутний паралелепіпед, усі три виміри якого рівні, називають кубом.

Усі грані куба – рівні квадрати.

Попередня тема

На початок

Наступна тема