МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

МНОГОГРАННИК ТА ЙОГО ЕЛЕМЕНТИ. ОПУКЛІ МНОГОГРАННИКИ. ПРИЗМА. ПРЯМА І ПРАВИЛЬНА ПРИЗМИ.

ПЕРЕРІЗ ПРИЗМИ. ПЛОЩА БІЧНОЇ ТА ПОВНОЇ ПОВЕРХОНЬ ПРИЗМИ

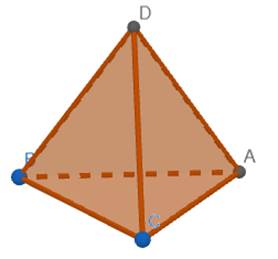
Многогранник та його елементи

У стереометрії вивчаються фігури у просторі, які прийнято називати тілами (або геометричними тілами). Геометричне тіло можна уявити як об’єднання частини простору, зайнятої фізичним тілом, та поверхні, яка обмежує цю частину простору.

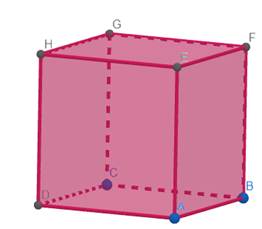
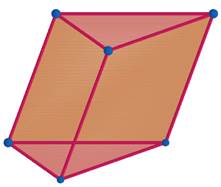
Многогранником називають тіло, поверхня якого складається зі скінченної кількості плоских многокутників.

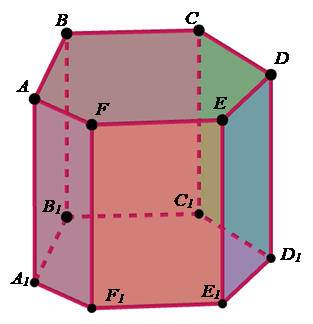
Многокутники, що обмежують многогранники, називають гранями. На малюнку многогранник складається з многокутників , , , , які є його гранями.

Сторони граней многогранника називають його ребрами (AB, BC, CD, DE, EF, A₁B₁, B₁C₁, C₁D₁, D₁E₁, E₁F₁, AA₁, BB₁, CC₁, DD₁, EE₁, FF₁).

Кінці ребер многогранника називаються його вершинами (А, B, C, D, E, F, А₁, B₁, C₁, D₁, E₁, F₁).

Дві грані многогранника називаються сусідніми, якщо вони мають спільне ребро, наприклад A₁ABB₁ та B₁BCC₁ має спільне ребро BB₁.

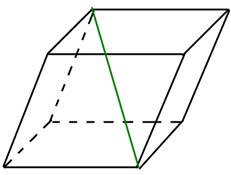
Відрізок, який сполучає дві вершини, що не належать одній грані, називається діагоналлю многогранника, наприклад BE₁.

Кут з вершиною грані многогранника називається плоским кутом многогранника при вершині

Двогранним кутом многогранника при ребрі A₁B₁ називають двогранний кут з ребром A₁B₁, грані якого містять сусідні грані многогранника, для яких ребро A₁B₁ є спільним.

Опуклі та неопуклі многогранники

Опуклі многогранники

Многогранник називають опуклим, якщо він розміщений по один бік від площини кожної його грані.

Неопуклі многогранники

Площа поверхні многогранника

Площа многогранника – це сума площ усіх його граней; вона дорівнює площі розгортки даного многогранника.

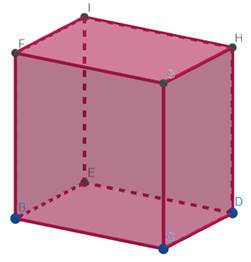
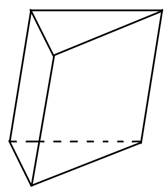
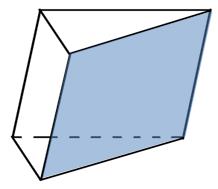
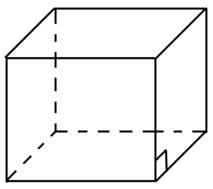
Призма. Пряма і правильна призми

	Многогранник, дві грані якого – рівні -кутники, що лежать у паралельних площинах, а решта граней – паралелограми, називають -кутною призмою.
	Бічні грані призми – паралелограми.
	Основи призми – рівні -кутники.
	Бічні ребра призми – ребра, які не належать основам (сусідні бічні грані призми – паралелограми, що мають спільну сторону – бічне ребро, то всі бічні грані призми є рівними та паралельними.)
	Ребра основ призми – сторони n-кутника .
	Висота призми – перпендикуляр, опущений з будь-якої точки площини однієї основи на площину іншої основи.
	Діагональ призми – відрізок, що сполучає дві вершини призми, які не належать одній грані.
Пряма призма Призма називається прямою, якщо її бічні ребра перпендикулярні до площини основи	Похила призма
	Правильна призма – пряма призма, в основі якої лежить правильний многокутник (рівносторонній трикутник, квадрат, шестикутник тощо).
	Діагональний переріз призми – переріз площиною, яка проходить через два бічних ребра, що не належать одній грані та діагональ основи.

Площа поверхні призми складається з площі бічної поверхні і двох площ основ призми:

– площа повної поверхні призми,

– площа бічної поверхні,

– площа основи призми.

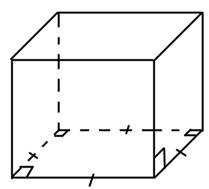
Теорема (про площу бічної поверхні прямої призми). Площа бічної поверхні прямої призми дорівнює добутку периметра її основи та бічного ребра призми.

Попередня тема

На початок

Наступна тема