МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

ЗАСТОСУВАННЯ ПОХІДНОЇ ДО ДОСЛІДЖЕННЯ ФУНКЦІЙ І ПОБУДОВИ ЇХ ГРАФІКІВ

Алгоритм дослідження графіка функції та побудова графіка

1. Знайти область визначення функції.

2. Дослідити функцію на парність, непарність та періодичність (для тригонометричних функцій).

3. Знайти точки перетину графіка функції з осями координат (якщо це можливо).

4. Знайти похідну та критичні точки функції.

5. Знайти проміжки зростання, спадання та екстремуми функції.

6. Дослідити поведінку функції на кінцях проміжків області визначення, якщо це можливо.

7. За потреби знайти ще кілька точок графіка та, використовуючи отримані результати, побудувати графік функції.

Приклад. Дослідити властивості функції та побудувати її графік.

Розв’язання.

1)

2) , отже функція ні парна, ні непарна.

3) Перетин з віссю Ох:

якщо , то

або

, після розв’язання квадратного рівняння маємо .

Отже, перетин з Ох в точках (-2; 0) та (1; 0).

Перетин з Оу:

Якщо , то Точка перетину з Оу (0; 2).

4)

Нехай

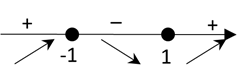
Тоді, – критичні точки.

5) Визначимо знак похідної на кожному з отриманих проміжків , , .

Функція зростає на проміжках та , спадає – на

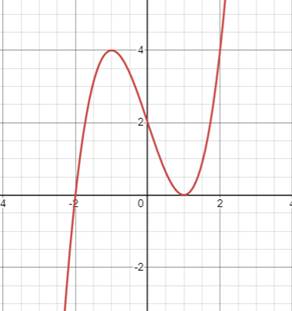
6) Будуємо графік функції, використовуючи результати дослідження:

Попередня тема

На початок

Наступна тема