|
Поняття сталості, зростання та спадання функції
|
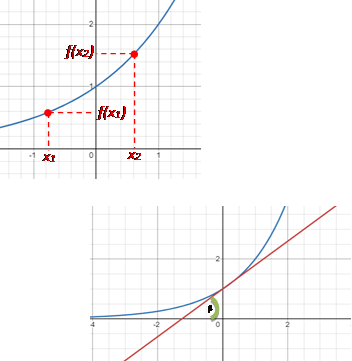
Функція називається зростаючою на проміжку,
якщо для будь-яких двох точок x₁ і x₂ з цього проміжку, таких що 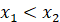 , виконується нерівність , виконується нерівність
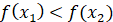 . .
Достатні умови зростання:
Якщо похідна функції 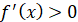 на
деякому проміжку, то функція на
деякому проміжку, то функція  зростає
на цьому проміжку. зростає
на цьому проміжку.
Геометрична
інтерпретація:
Якщо дотична до графіка функції в точці утворює гострий кут з додатним напрямком осі Ox, то функція зростає в цій точці.
|
|
|
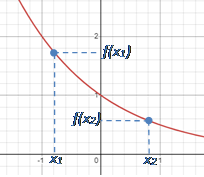
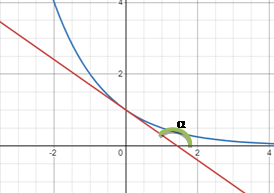
Функція називається спадною на проміжку, якщо для будь-яких двох точок x₁ і x₂ з цього проміжку, таких що 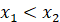 , виконується нерівність , виконується нерівність
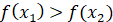 . .
Достатні умови спадання:
Якщо похідна функції 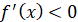 на
деякому проміжку, то функція на
деякому проміжку, то функція  спадає
на цьому проміжку. спадає
на цьому проміжку.
Геометрична
інтерпретація:
Якщо дотична до графіка функції в точці утворює тупий кут з додатним напрямком осі Ox, то функція спадає в цій точці.
|
|
|
Функція називається сталою на проміжку, якщо для будь-яких двох точок x₁ і x₂ з цього проміжку значення функції рівні, тобто 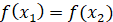 . .
Геометрична
інтерпретація:
Якщо дотична до графіка функції в точці паралельна осі Ox, то функція стала в цій точці.
|
 
|
Екстремуми (максимуми і
мінімуми) функції
|
|
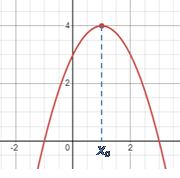
Точка x₀ називається точкою
максимуму функції f(x), якщо існує окіл точки x₀, такий, що для всіх x з цього околу виконується нерівність 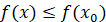 . .
|
|
|
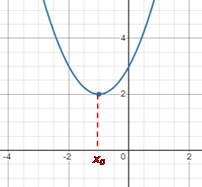
Точка x₀ називається точкою
мінімуму функції f(x),
якщо існує окіл точки x₀, такий, що для всіх x з цього околу виконується нерівність
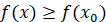 . .
|
|
Точки
максимуму та мінімуму називаються
точками екстремуму.
|
|
Необхідна умова екстремуму:
|
|
Якщо в точці x₀ функція f(x) має екстремум, то її похідна в цій точці дорівнює нулю або не існує: f'(x₀) = 0 або f'(x₀) не існує.
|
|
Достатня умова екстремуму:
|
|
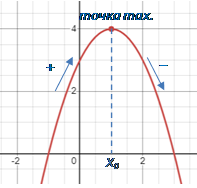
|
Якщо при переході через точку x₀ похідна функції змінює знак з «+» на
«–», то в точці x₀ функція має максимум.
|
|
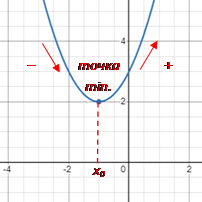
|
Якщо при переході через точку x₀ похідна функції змінює знак з «–» на «+», то в точці x₀ функція має мінімум.
|
Алгоритм
дослідження функції 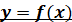 на монотонність та екстремуми функції на монотонність та екстремуми функції
за допомогою похідної
|
Алгоритм
|
Приклад
Знайдіть проміжки монотонності, точки екстремуму
та екстремути функції
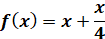
|
|
Знайти область визначення функції
|
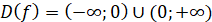
|
|
Знайти похідну функції
|
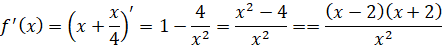
|
|
Знайти критичні точки функції
|
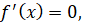 тобто тобто
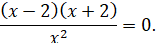
Тоді, х1=2; х2= –2 – критичні точки.
|
|
Поділити знайденими критичними точками область визначення
функції на проміжки та з’ясувати знак похідної на
кожному з них
|
Визначимо знак похідної на
кожному з отриманих проміжків:
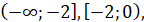 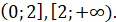

|
|
üЯкщо 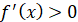 в кожній
точці проміжку, то функція в кожній
точці проміжку, то функція 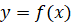 зростає на даному проміжку. зростає на даному проміжку.
üЯкщо 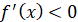 в кожній
точці проміжку, то функція в кожній
точці проміжку, то функція 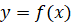 спадає на даному проміжку. спадає на даному проміжку.
|
Функція зростає на проміжках 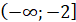 і і 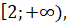 спадає
на проміжках спадає
на проміжках 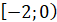 і і 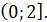
|
|
üЯкщо у критичній точці
х0 похідна змінює
знак з «+» на «–», то 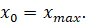
üЯкщо у критичній точці
х0 похідна змінює
знак з «–» на «+», то 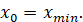
üЯкщо зміни знаків немає, то х0 – не є точкою екстремуму.
|
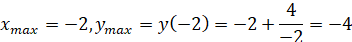
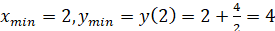 . .
|
|








