|
Фізичний зміст похідної
|

|
Нехай
авто рухається за певним законом 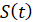
Середня швидкості руху
тіла 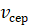 – це
фізична величина, що дорівнює відношенню всього шляху S, який пройшло тіло, до інтервалу часу t,
за який цей шлях пройдено: – це
фізична величина, що дорівнює відношенню всього шляху S, який пройшло тіло, до інтервалу часу t,
за який цей шлях пройдено:
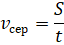
|
|
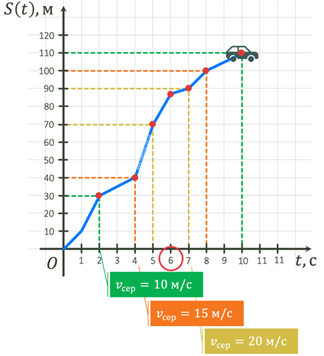
Наприклад, знайдемо середню швидкість авто на різних проміжках, а
саме на проміжках часу 2–10 секунди,
4–8 секунди, 5–7 секунди:
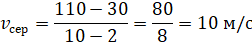
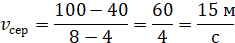
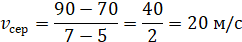
|
|
|
|
|
|
|
|
|
Фізичний зміст
похідної: Якщо відомий закон руху 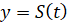 , то швидкість , то швидкість
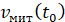 дорівнює похідній цієї функції дорівнює похідній цієї функції
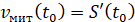 . .
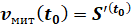
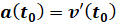
*Для
знаходження прискорення достатньо взяти похідну від швидкості
Завдання
1
Електросамокат рухається за законом 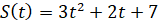 . Знайдіть швидкість і прискорення цього самокату на 4-й секунді його
руху. . Знайдіть швидкість і прискорення цього самокату на 4-й секунді його
руху.
Розвʼязання:
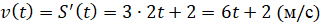
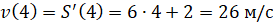
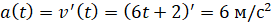 (тобто прискорення
є сталим на всьому проміжку шляху) (тобто прискорення
є сталим на всьому проміжку шляху)
Відповідь:
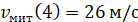
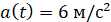
Дотична до графіка функції
|
|
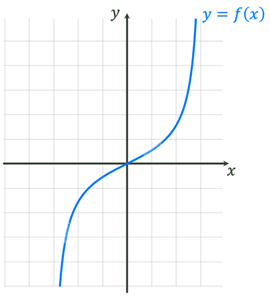
Як ви
розумієте поняття «дотична до графіка функції»
Дотичною до графіка функції в точці x0 називають пряму,
яка дотикається до цього графіка в точці x0.
На
рисунку, пряма 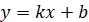 – дотична до графіка – дотична до графіка
|
|
Як бачимо, дотична може мати з графіком функції більше однієї спільної
точки. Зауважимо, що загальним виглядом будь-якої не вертикальної дотичної
завжди буде пряма виду 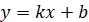
Отже, уведемо поняття дотичної в точці до
графіка функції.
|
|
|
|
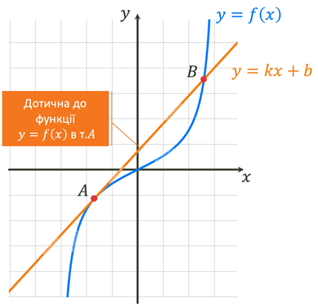
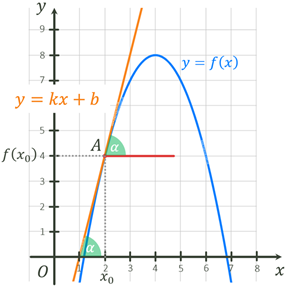
Оскільки рівняння прямої 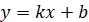 , то можемо
зробити висновок про геометричний зміст похідної: , то можемо
зробити висновок про геометричний зміст похідної:
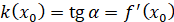
Тобто кутовий коефіцієнт дотичної до графіка функції 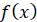 , проведеної в точці з абсцисою , проведеної в точці з абсцисою 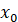 , дорівнює похідній функції у цій точці. , дорівнює похідній функції у цій точці.
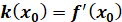
|
|
|
|
|
|
|
|
Рівняння
дотичної до графіка функції
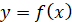 у
точці з абсцисою у
точці з абсцисою 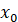 має
вигляд: має
вигляд:
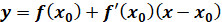
Завдання
2.
Складіть рівняння
дотичної до графіка функції 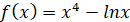 у точці з
абсцисою у точці з
абсцисою 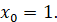
Розв’язання:
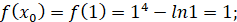
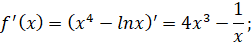
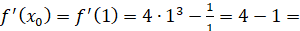 3 3
Підставимо отримані значення в рівняння дотичної 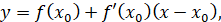 отримаємо: отримаємо:
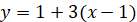 , тобто , тобто 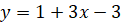 , отже, , отже,  . .
Завдання
3. Знайдіть кутовий коефіцієнт дотичної,
проведеної до графіка функції 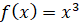 у точці з
абсцисою у точці з
абсцисою 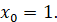
Розв’язання:
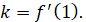 Оскільки Оскільки 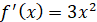 , то , то  . .
|




