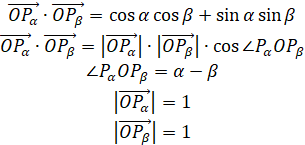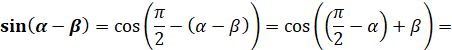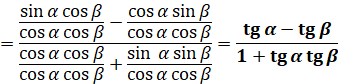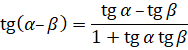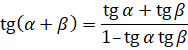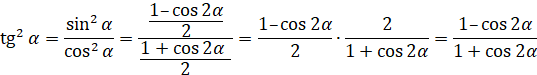МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

ТРИГОНОМЕТРИЧНІ ФОРМУЛИ ДОДАВАННЯ. ФОРМУЛИ ПОДВІЙНОГО І ПОЛОВИННОГО КУТА.

ФОРМУЛИ ПОНИЖЕННЯ СТЕПЕНЯ

Тригонометричні формули додавання

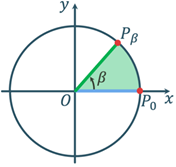
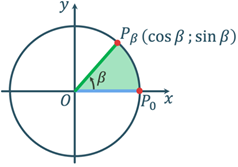
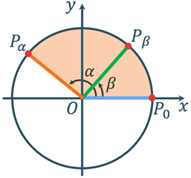
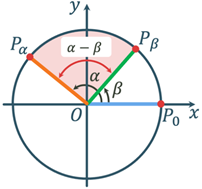
Þ Косинус різниці і суми аргументів

	При повороті на кут початковий радіус одиничного кола перейшов у радіус . Матимемо координати точки :
Координатами вектора будуть координати точки :
	При повороті на кут α координати вектора матимуть координати
Виразимо скалярний добуток векторів і через їх координати
та через теорему про скалярний добуток векторів.
	Прирівняємо два вирази:
Маємо формулу косинуса різниці
З формули косинуса різниці можна отримати формулу косинуса суми, якщо у формулу косинуса різниці замість кута «» підставити кут «».

Формули косинуса різниці і суми аргументів:

Þ Синус різниці і суми аргументів

Формулу синуса різниці аргументів виведемо за допомогою формули зведення:

Доведення:

	Доведено.

Аналогічно виведемо формулу синуса суми аргументів:

Доведення:

	Доведено.

Формули синуса різниці і суми аргументів:

Þ Тангенс різниці і суми аргументів

Формула тангенса різниці аргументів:

Доведення: для доведення скористаємося залежністю

	За умови, що
	Доведено.

Формула тангенса суми аргументів:

Доведення:

	Доведено.

Формули тангенса різниці і суми аргументів:

Формули подвійного і половинного кута

Þ Формули подвійного кута

Запишимо формулу синуса суми аргументів, при :

Запишимо формулу косинуса суми аргументів, при :

Скориставшись основною тригонометричною тотожністю і формулою косинуса подвійного кута, можна отримати ще дві формули для косинуса подвійного кута:

Запишимо формулу тангенса подвійного кута, при :

Þ Формули пониження степеня

Виразимо і з вже відомих формул косинуса подвійного кута:

Знайдемо формулу пониження степеня для тангенса, використовуючи формули пониження степеня синуса і косинуса:

Þ Формули половинного аргументу

Підставимо у формули пониження степеня кут замість кута :

Попередня тема

На початок

Наступна тема