|
Періодичність функцій
Функція 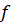 називається періодичною,
якщо існує таке число називається періодичною,
якщо існує таке число 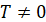 , що для
будь-якого , що для
будь-якого 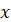 з області визначення функції з області визначення функції 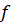 виконуються рівності: виконуються рівності:
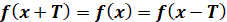
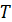 – період функції. – період функції.
Оскільки, значення синуса і косинуса повторюються як
мінімум через один оберт, то:
|
Найменший період 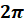
|
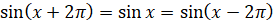
|
Інші періоди,
кратні 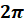 : :
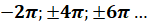
|
|
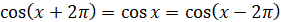
|
Поглянувши на лінію тангенсів і лінію контангесів, ми бачимо, що значення тангенса і
котангенса повторюється як мінімум
через кожні пів оберта, тому:
|
Найменший період 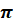
|
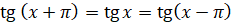
|
Інші періоди, кратні 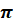 : :
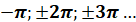
|
|
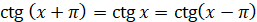
|
Графік функції 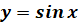 та її властивості та її властивості
1.
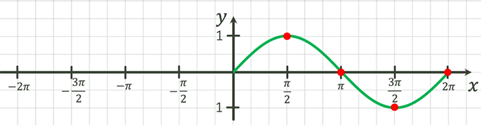
Побудуємо
систему координат, взявши за одиницю довжини 2 клітинки.
2. Так як число 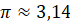 , то для зручності позначення числа , то для зручності позначення числа 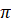 візьмемо 6 клітинок. візьмемо 6 клітинок.
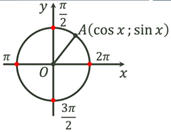
3. Проаналізуємо, яким значенням на
одиничному колі відповідає 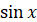 та позначимо ці точки на нашій системі
координат. та позначимо ці точки на нашій системі
координат.
4.
Зʼєднаємо ці точки
плавною лінією.
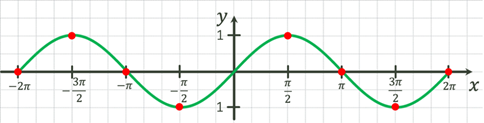
5. Так як функція 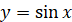 є
непарною, то її графік симетричний відносно початку координат. Виконавши
симетричне відображення функції, отримаємо графік фукнції є
непарною, то її графік симетричний відносно початку координат. Виконавши
симетричне відображення функції, отримаємо графік фукнції
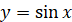 на
проміжку на
проміжку 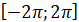 . .
6. Графік функції 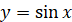 називається синусоїдою. називається синусоїдою.
Властивості
функції 
|
Область
визначення
|
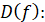
|
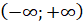
|
|
Множина
значень
|
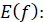
|
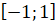
|
|
Парність,
непарність
|
Непарна
|
|
|
Найменший додатний період:
|
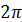
|
|
|
Нулі функції:
|
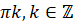
|
|
|
Знакосталість, 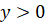 : :
|
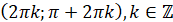
|
|
|
Знакосталість, 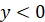 : :
|
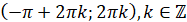
|
|
|
Проміжки зростання:
|
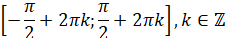
|
|
|
Проміжки спадання:
|
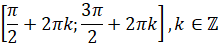
|
|
|
Найбільше значення функції:
|
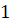 при при 
|
|
|
Найменше значення функції:
|
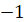 при при 
|
|
|
|
|
|
|
Графік функції 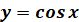 та її властивості та її властивості
Графік функції 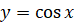 можна отримати так
само, як і графік функції можна отримати так
само, як і графік функції 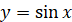 , а можна скористатися формулами
зведення, а саме тим, що , а можна скористатися формулами
зведення, а саме тим, що 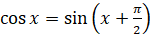 . Тобто
графік функції . Тобто
графік функції 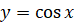 можна отримати за допомогою паралельного
перенесення графіка можна отримати за допомогою паралельного
перенесення графіка 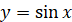 вздовж осі абсцис ліворуч на вздовж осі абсцис ліворуч на  . .
|
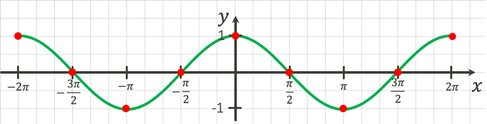
Косинусоїда
|
|
|
|
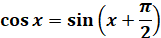
|
|
Зсув графіка 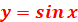 на на  ліворуч ліворуч
|
|
Властивості
фукнції 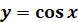
|
Область
визначення
|
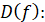
|
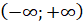
|
|
Множина
значень
|
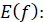
|
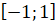
|
|
Парність,
непарність
|
Парна
|
|
Найменший додатний період:
|
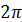
|
|
Нулі функції:
|
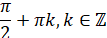
|
|
Знакосталість, 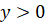 : :
|
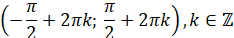
|
|
Знакосталість, 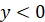 : :
|
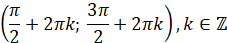
|
|
Проміжки зростання:
|
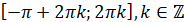
|
|
Проміжки спадання:
|
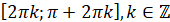
|
|
Найбільше значення функції:
|
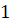 при при 
|
|
Найменше значення функції:
|
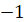 при при 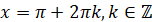
|
Графік функції  та її
властивості та її
властивості
|
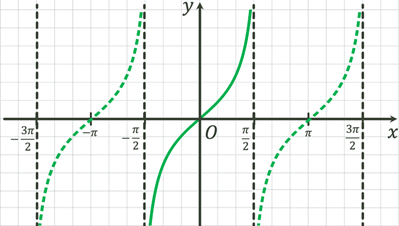
Тангенсоїда
|
|
|
|
Графік функції 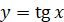 можна
отримати так само, як і графік функції можна
отримати так само, як і графік функції 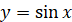 . .
Оскільки, значення
тангенса у точках  і і 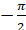 не існує, то це значення при наближенні до даних точок може бути як
завгодно малим, але ніколи не буде дорівнювати даним значенням. не існує, то це значення при наближенні до даних точок може бути як
завгодно малим, але ніколи не буде дорівнювати даним значенням.
|
|
Графік функції 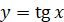 складається з безлічі окремих гілок – гілок
тангенсоїди. складається з безлічі окремих гілок – гілок
тангенсоїди.
|
Властивості
фукнції 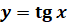
|
Область визначення
|
|
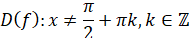
|
|
Множина значень
|
|
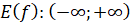
|
|
Парність, непарність
|
Непарна
|
|
Найменший додатний період:
|
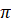
|
|
Нулі функції:
|
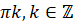
|
|
Знакосталість, 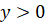 : :
|
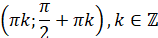
|
|
Знакосталість, 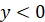 : :
|
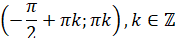
|
|
Проміжки зростання:
|
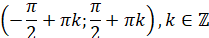
|
|
Проміжки спадання:
|
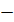
|
|
Найбільше значення функції:
|
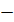
|
|
Найменше значення функції:
|
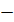
|
Графік
функції 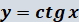 та її
властивості та її
властивості
|
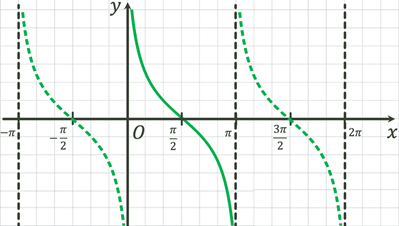
Котангенсоїда
|
|
|
|
Для побудови функції 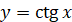 , аналогічно, як і для функції , аналогічно, як і для функції 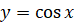 , скористаємося формулами зведення. , скористаємося формулами зведення.
Оскільки  , то графік , то графік 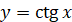 можна отримати, якщо
виконаємо паралельне перенесення графіка можна отримати, якщо
виконаємо паралельне перенесення графіка 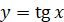 ліворуч вздовж осі абсцис, а
потім симетрично відобразимо його відносно цієї осі. ліворуч вздовж осі абсцис, а
потім симетрично відобразимо його відносно цієї осі.
|
Властивості
фукнції 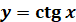
|
Область визначення
|
|
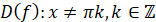
|
|
Множина значень
|
|
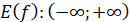
|
|
Парність, непарність
|
Непарна
|
|
Найменший додатний період:
|
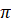
|
|
Нулі функції:
|
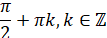
|
|
Знакосталість, 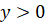 : :
|
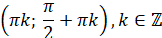
|
|
Знакосталість, 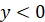 : :
|
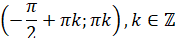
|
|
Проміжки зростання:
|
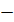
|
|
Проміжки спадання:
|
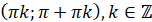
|
|
Найбільше значення функції:
|
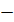
|
|
Найменше значення функції:
|
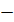
|
Властивість періодичних функцій
|
Найменший додатний
період функцій 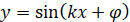 і і 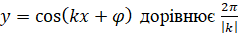
|
|
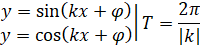
|
|
Найменший додатний період функцій 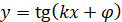 і і 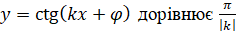
|
|

|
|
|
|
|