|
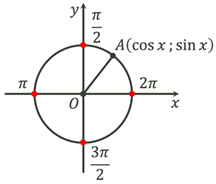
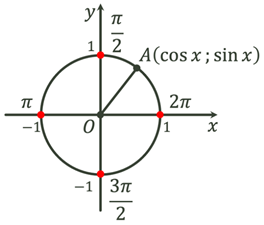
Область визначення тригонометричних функцій
Множина значень тригонометричних функцій
|
Множина значень
|
|
|
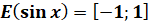
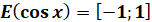
|
|
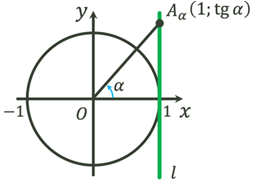
|
Ордината т. 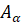 дорівнює тангенсу дорівнює тангенсу
кута 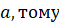
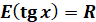
|
|
Абсциса т. 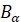 дорівнює котангенсу дорівнює котангенсу
кута 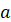 , тому , тому
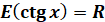
|
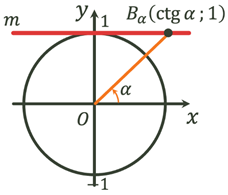
|
Знаки тригонометричних функцій
|
Координати по осі абсцис одиничного кола – це значення косинуса, координати по осі ординат – значення синуса)
|
|
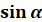
|
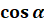
|
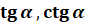
|
|
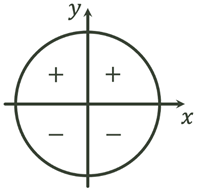
В І та ІІ чвертях sinα>0
В ІІІ та IV чвертях sinα<0
|
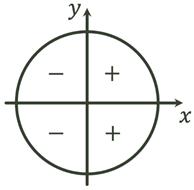
В І та ІV чвертях cosα>0
В ІІ та III чвертях cosα<0
|
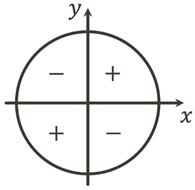
В І та ІIІ чвертях tgα>0, ctg>0
В ІІ та IV чвертях tgα<0, ctg<0
|
Парність і непарність тригонометричних фукнцій
|
|
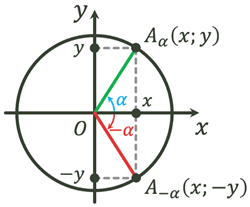
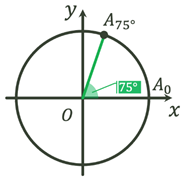
Точки 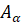 і і 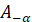 симетричні, так як при повороті
на кут симетричні, так як при повороті
на кут 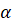 початковий радіус одиничного кола
переходить у точку початковий радіус одиничного кола
переходить у точку 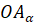 , а на кут , а на кут 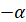 – у
радіус – у
радіус 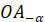 , отже абсциси точок , отже абсциси точок 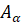 і і 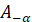 будуть
однаковими, а ординати – різними. Отже: будуть
однаковими, а ординати – різними. Отже:
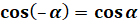
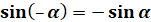
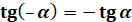
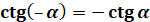
|
|
Тому,
Косинус –
парна функція.
Синус, тангенс і котангенс – непарні функції.
|
Періодичність тригонометричних функцій
|
Періоди синуса і косинуса
|
|
|
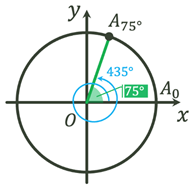
При повороті на кут  початковий радіус початковий радіус 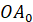 переходить у радіус переходить у радіус 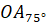 . Щоб отримати цей самий радіус . Щоб отримати цей самий радіус 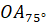 необхідно повернути
початковий радіус необхідно повернути
початковий радіус 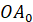 на кут на кут 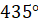 , тобто на один повний оберт , тобто на один повний оберт 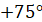 . Отже при зміні кута на ціле число обертів ( . Отже при зміні кута на ціле число обертів (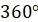 або або 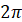 радіан) значення тригонометричних функцій
синуса і косинуса змінюватися не будуть. радіан) значення тригонометричних функцій
синуса і косинуса змінюватися не будуть.
|
|
|
Всі функції, що мають таку властивість, називаються періодичними.
Кожна періодична функція має безліч періодів. Наприклад, функції синус і косинус мають
періоди 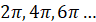
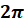 – найменший період
синуса і косинуса. – найменший період
синуса і косинуса.
|
|
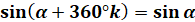
|
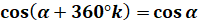
|
|
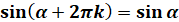
|
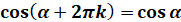
|
|
|
|
|
Періоди тангенса і котангенса
|
|

|
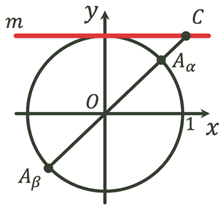
Розглянемо радіуси  і і 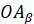 , що утворються внаслідок повороту початкового
радіуса на кути , що утворються внаслідок повороту початкового
радіуса на кути 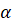 і і 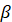 . Точки . Точки 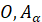 і і 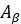 лежать
на одній прямій, отже прямі лежать
на одній прямій, отже прямі 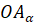 та та 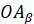 перетинають вісь тангенсів в одній точці –
точці перетинають вісь тангенсів в одній точці –
точці 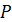 . Отже два різні кути мають одне значення. Тому
тангенс при зміні кута на ціле число півобертів не буде змінювати свого
значення. . Отже два різні кути мають одне значення. Тому
тангенс при зміні кута на ціле число півобертів не буде змінювати свого
значення.
|
|
Таким самим
чином можна показати, що котангес не буде змінювати свого значення при повороті на ціле число півобертів.
|
|
|
Тому, 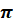 – найменший
період тангенса
і котангенса – найменший
період тангенса
і котангенса
|
|
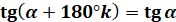
|
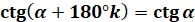
|
|
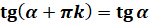
|
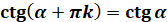
|
|
|
|
|
|
|
|
|