|
Означеня синуса, косинуса, тангенса, котангенса гострого
кута
прямокутного трикутника
|

|
Синус гострого кута прямокутного трикутника – це відношення протилежного катета до
гіпотенузи
|
|

|
|
Косинус гострого кута прямокутного трикутника – це відношення прилеглого катета до
гіпотенузи
|
|

|
|
Тангенс гострого кута прямокутного трикутника – це відношення протилежного катета до
прилеглого катета
|
|

|
|
Котангенс гострого кута прямокутного трикутника – це відношення прилеглого катета до
протилежного катета
|
|
|

|
Означеня синуса, косинуса, тангенса за допомогою одиничного
кола
|

|
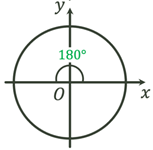
Одиничне півколо – півколо з центром в початку координат, що побудоване в I і II координатній чвертях, з радіусом 1.
|
|
Одиничне півколо
|
|
|

|

|
|
Косинус і синус кута  , , 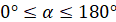 – це відповідні абсциса і ордината точки – це відповідні абсциса і ордината точки  одиничного півкола, яка
відповідає куту одиничного півкола, яка
відповідає куту 
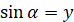

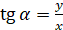 

|
Як за допомогою означення синуса і
косинуса знайти координати т. 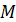 ,
якщо радіус не дорівнює ,
якщо радіус не дорівнює 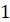 ? ?
|

|
Синусом кута 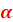 називається відношення ординати кінця
рухомого радіуса, що утворює цей кут з додатною піввіссю називається відношення ординати кінця
рухомого радіуса, що утворює цей кут з додатною піввіссю 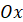 , до довжини цього
радіуса. , до довжини цього
радіуса.

|
|
Косинусом кута 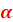 називається відношення абсциси кінця
рухомого радіуса, що утворює цей кут з додатною піввіссю називається відношення абсциси кінця
рухомого радіуса, що утворює цей кут з додатною піввіссю 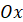 , до довжини цього
радіуса. , до довжини цього
радіуса.

|
|
Тангенсом кута 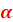 називається відношення ординати кінця рухомого радіуса, що утворює
цей кут з додатною піввіссю називається відношення ординати кінця рухомого радіуса, що утворює
цей кут з додатною піввіссю 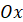 , до його абсциси. , до його абсциси.
|
|

|

|

|
|
Котангенсом кута 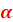 називається відношення абсциси кінця рухомого радіуса, що утоворює цей кут з додатною піввіссю називається відношення абсциси кінця рухомого радіуса, що утоворює цей кут з додатною піввіссю 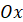 , до його ординати. , до його ординати.
|
|

|

|

|
|
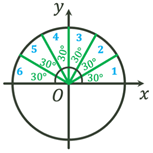
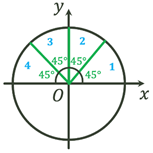
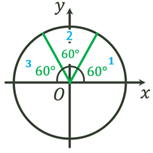
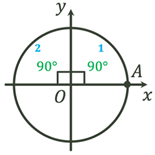
Побудова кута довільної величини
Якщо у колі із центром у початку координат 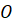 обертати радіус обертати радіус 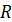 навколо т. навколо т.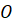 , то можуть
утворюватися як додатні кути повороту, так і відʼємні
кути повороту. , то можуть
утворюватися як додатні кути повороту, так і відʼємні
кути повороту.
|

|
Додатній кут повороту – поворот, протилежний руху годинникової стрілки.
|

|
|
Відʼємний кут повороту – поворот в напрямі
руху годинникової стрілки.
|

|
Градусна
міра кутів

Одиниця виміру кутів –  ; ;
Градусна міра розгорнутого кута –  ; ;
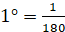 частина
розгорнутого кута; частина
розгорнутого кута;
Вимірювання дуже малих кутів
|
Мінута – це 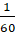 частина частина 
|
Позначення: 
|
|
Секунда – це 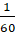 частина частина 
|
Позначення: 
|
Радіанна
міра кута
|

|
1 радіан – центральний кут,
що відповідає дузі кола, довжина якої дорівнює радіусу кола.
|
|

|

|
|

|
|

|

|
|
|
|
|
Чому 
|
|

|

|
|
 – довжина дуги, що дорівнює – довжина дуги, що дорівнює  ; ;
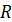 – довжина дуги, що дорівнює 1 рад; – довжина дуги, що дорівнює 1 рад;
Отже півколо вміщує в собі  радіан. радіан.
|
Тригонометричні
функції числового аргументу
|
Градусна міра кута
|

|

|

|

|

|

|

|
|
Радіанна міра кута
|

|

|

|

|

|

|

|
Так як
кожному допустимому значенню числа 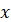 ( (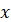 – кут,
що містить – кут,
що містить 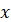 радіанів) відповідає єдине значення радіанів) відповідає єдине значення 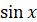 , , 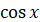 , , 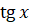 , ,  , то синус, косинус, тангенс і котангенс є функціями числового аргементу , то синус, косинус, тангенс і котангенс є функціями числового аргементу
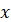 . Такі функції називаються тригонометричнимим функціями числового аргументу. . Такі функції називаються тригонометричнимим функціями числового аргументу.
Значення тригонометричних функцій
деяких кутів
|
α, рад
|
0
|

|

|

|

|

|

|

|
|
α, град
|
0
|

|

|

|

|

|

|

|
|
sin α
|
0
|

|

|

|
1
|
0
|
–1
|
0
|
|
cos α
|
1
|

|

|

|
0
|
–1
|
0
|
1
|
|
tg α
|
0
|

|
1
|

|
–
|
0
|
–
|
0
|
|
ctg α
|
–
|

|
1
|

|
0
|
–
|
0
|
–
|
|
|
|
|
|
|
|
|