МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

МОНОТОННІСТЬ, ПАРНІСТЬ І НЕПАРНІСТЬ ФУНКЦІЙ. НЕПЕРЕРВНІСТЬ ФУНКЦІЙ

Функція називається зростаючою, якщо більшому значенню аргументу відповідає більше значення функції.
Функція називається спадною, якщо більшому значенню аргументу відповідає менше значення функції

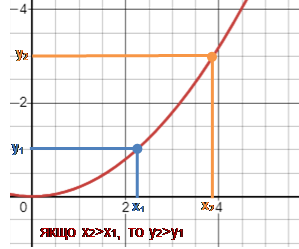
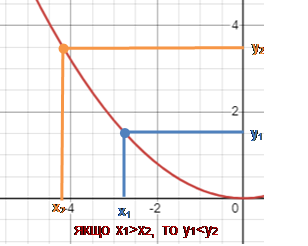
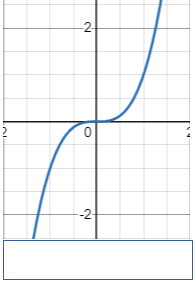
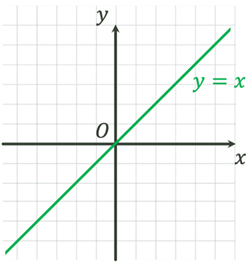
Функція називається монотонною на деякому проміжку, якщо вона на цьому проміжку або зростає, або спадає.

Проміжки зростання або спадання функції називаються проміжками монотонності.

Область визначення симетрична відносно нуля.	Область визначення несиметрична відносно нуля.
Для кожного додатного числа області визначення, міститься також і число .	Для чисел і область визначення не містить чисел і
– парна	– непарна
Графік парної функції симетричний відносно осі (ординат)	Графік непарної функції симетричний відносно початку координат

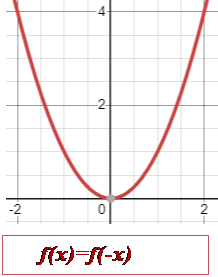
Алгоритм дослідження функції на парність і непарність:

1. Перевірити, чи симетрична область визначення відносно нуля.

2. Перевірити виконання умови: або

(!) Не будь-яка функція може бути парною або непарною.

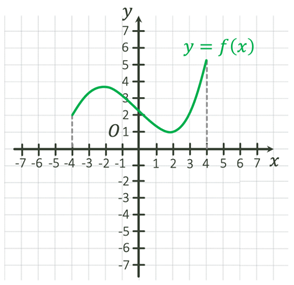
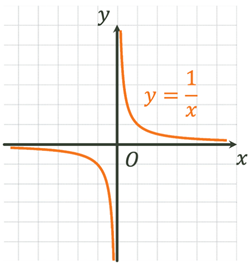
Якщо не виконується хоча б одна з умов алгоритму дослідження функції на парність і непарність, то функція є ні парною ні непарною. Кажуть, що вона є індиферентною.

Функція неперервна на проміжку, якщо її графік на цьому проміжку – неперервна лінія.

Неперервна на проміжку	Неперервна на проміжках і
	Точка – точка розриву
	(Точка не належить області визначення даної функції)

Попередня тема

На початок

Наступна тема