|
Функція – це таке правило, за якого кожному значенню незалежної змінної з деякої
множини відповідає єдине значення залежної змінної.
|
|

|
Область визначення функції 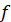 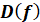 – це множина тих значень, яких може
набувати аргумент 𝑥 – це множина тих значень, яких може
набувати аргумент 𝑥
|
|
Область значень функції 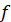 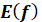 – це множина, яка
складається із всіх чисел – це множина, яка
складається із всіх чисел 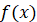 , де , де 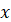 належить області визначення належить області визначення
|
|
Функція називається числовою, якщо її область значень і область
визначення – числа.
|
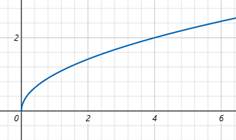
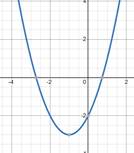
Властивості функції
Розглянемо
властивості функції на прикладі квадратичної функції 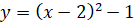 графіком якої є парабола. графіком якої є парабола.
|
|
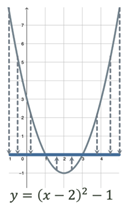
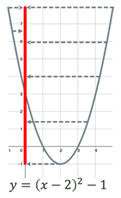
Область
визначення (множина значень
аргументу, при яких задана функція)
|
Проєкція графіка на вісь 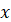
|
|
|
|
Область
значень (множина чисел, що складаються із всіх значень функції)
|
Проєкція графіка на вісь 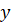
|
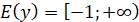
|
|
|
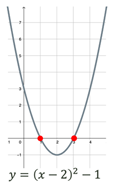
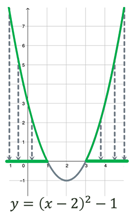
Нулі функції (точки, в яких
значення функції дорівнює нулю), або
розвʼязок 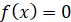
|
Точки перетину графіка
функції з віссю 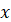
|
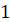 і і 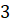
|
|
|
Проміжки
знакосталості (проміжки, на яких функція додатна або відʼємна), або розвʼязки 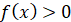 і і 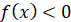
|
Проєкція графіка функції,
що знаходиться вище або нижче осі  , на вісь , на вісь 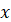
|
Додатні значення ф-ї: 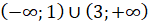
|
|
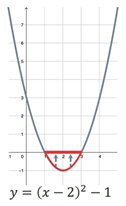
|
|
|
Відʼємні значення ф-ї: 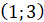
|
|
|
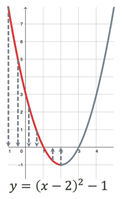
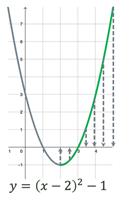
Проміжки
зростання та спадання функції (проміжки, на яких функція або зростає,
або спадає)
|
Проєкція графіка функції,
що іде вгору або вниз, на вісь 
|
Ф-я спадає на проміжку: 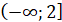
|
|
|
|
|
Ф-я зростає на проміжку: 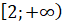
|
Способи задання функцій
1. Аналітичний
– функцію задано формулою
Приклади
функцій:
|
Площа круга:
|
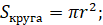 де де
  аргумент, аргумент, 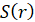 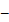 функція. функція.
|
|
Капітал, що можна отримати,
якщо вкласти певну суму грошей на певну кількість років до банку:
|
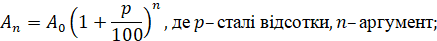
|
|
Довільні функції
|
|
|
|
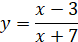
|
2. Табличний – за допомогою таблиці
Наприклад,
|
Розмір
файлу, Мб
|
400 Мб
|
700 Мб
|
1000 Мб
|
|
Час завантаження
при швидкості 100 кбіт/с
|
9 год 9 хв 15 с
|
16 од 18 хв 41 с
|
23 од 18 хв 7 с
|
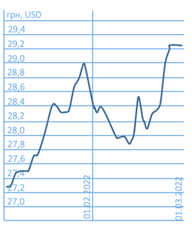
3. Графічний – за допомогою графіка
Наприклад,
|
Зміна курсу валюти
|
Кардіограма
|
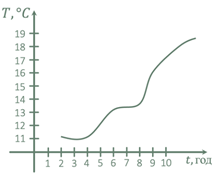
Зміна температури повітря
|
|
|
|
|
|
|
|
|
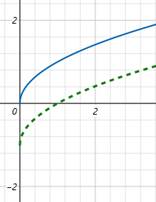
Перетворення графіків функцій
Розглянемо перетворення графіків функції на прикладі функцій
|
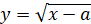
|
Паралельне перенесення графіка на a одиниць вздовж осі Ох
(при a>0 – праворуч,
при a<0 – праворуч)
|
|
|
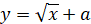
|
Паралельне перенесення графіка на a одиниць вздовж осі Оу
(при a>0 – вгору)
|
|
|
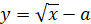
|
Паралельне перенесення графіка на a одиниць вздовж осі Оу
(при a<0 – донизу)
|
|
|
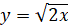
|
Графік функції 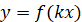 , де k>0, отримується із графіка функції , де k>0, отримується із графіка функції  стисненням його вздовж осі Ох у k разів, якщо k>1; розтягом його вздовж осі Ох у стисненням його вздовж осі Ох у k разів, якщо k>1; розтягом його вздовж осі Ох у  разів, якщо разів, якщо
0 < k < 1.
|
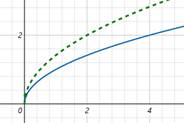
|
|
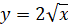
|
Графік функції 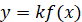 , де k>0, отримується із графіка функції , де k>0, отримується із графіка функції 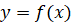 розтягом його вздовж осі Оy у k разів, якщо k>1; стисненням його вздовж осі Оy у розтягом його вздовж осі Оy у k разів, якщо k>1; стисненням його вздовж осі Оy у  разів, якщо разів, якщо
0 < k < 1.
|
|
|

|
Графік функції 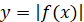 отримується із графіка функції отримується із графіка функції 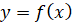 за допомогою дій: за допомогою дій:
- вище осі Ох
(і на самій осі) залишають його без змін;
- нижче осі Ох
– симетрично відображають
його відносно осі Ох.
|
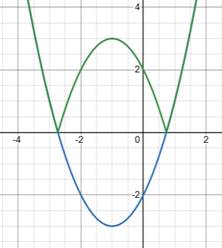
|
|
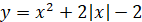
|
Графік функції 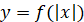 отримується із графіка
функції отримується із графіка
функції 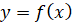 за допомогою дій: за допомогою дій:
- справа від осі Оу
(і на самій осі) залишають без змін і симетрично відображають цю частину відносно осі Оу.
|
|
|