МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

КОРІНЬ n-ГО СТЕПЕНЯ. АРИФМЕТИЧНИЙ КОРІНЬ n-ГО СТЕПЕНЯ

Коренем (алгебраїчним) -го степеня із числа називають таке число, -й степінь якого дорівнює .

– показник кореня, – знак кореня (радикал), – підкореневий вираз

Арифметичний корінь існує тільки для невідʼємного числа і може дорівнювати тільки невідʼємному числу (!)

Наприклад,

Алгебраїчні корені
Арифметичний корінь

Тобто, якщо , , , то вираз означає арифметичний корінь -го степеня із числа .

	ОДЗ для функції :
– не парне			, так як
– парне			Не існує на (немає такого числа, яке при піднесенні до парного степеня дає відʼємне число)

Тотожності для кореня -го степеня

	– не парне		Наприклад:
	– парне
	Тільки для коренів непарного степеня (!)		Наприклад:

Остання тотожність дає можливість виразити не алгебраїчний корінь з відʼємного числа як алгебраїчний корінь того ж степеня:

// не алгебраїчний корінь;	// алгебраїчний корінь

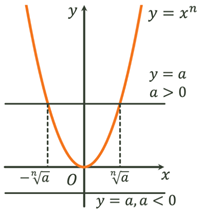
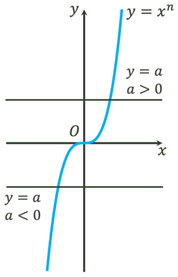
Рівняння

		Коренів немає
Наприклад:				Наприклад:
		Коренів немає

Попередня тема

На початок

Наступна тема