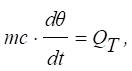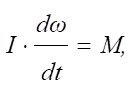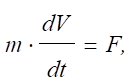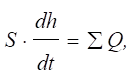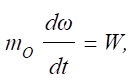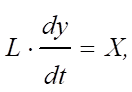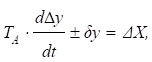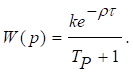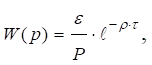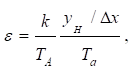АВТОМАТИЗАЦІЯ ТЕХНОЛОГІЧНИХ ПРОЦЕСІВ

І СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ

Електронний посібник

ГОЛОВНА	ТЕОРЕТИЧНІ ВІДОМОСТІ	АНОТАЦІЯ
ДОДАТКИ	СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

1. ОСНОВИ АВТОМАТИЗАЦІЇ СІЛЬСЬКОГОСПОДАРСЬКОГО ВИРОБНИЦТВА

1.5. Розробка та аналіз математичної моделі об’єкта керування

Під час розробки систем автоматизації кожний технологічний процес, машина, устаткування, апарат, що підлягає автоматизації, називаються об'єктами автоматизації. Об'єкт автоматизації – це одне із центральних понять у теорії автоматичного регулювання та управління.

Його властивості визначають склад комплексу технічних засобів та алгоритм управління. Тобто, об'єкт автоматизації можна розглядати як деякий базис, а всі інші елементи системи як надбудову.

Рис. 1.5.1. Технологічний процес – доїння корів

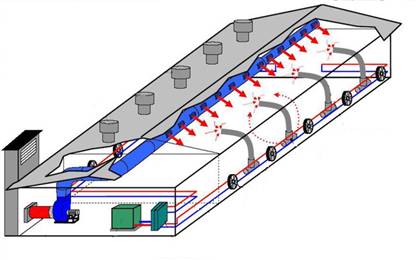
У сільськогосподарському виробництві найсприятливіші умови для автоматизації забезпечуються для стаціонарних процесів у тваринництві, закритому ґрунті, переробки та зберігання сільськогосподарської продукції. Останнім часом завдяки розвиткові мікроелектроніки стала можливою автоматизація мобільної техніки: тракторів, комбайнів, сівалок.

Таким чином, об'єктами автоматизації у сільському господарстві є:

· технологічні процеси (створення мікроклімату, приготування та роздача кормів, сушіння та очищення продукції, стабілізація рівня рідин),

· окремі механізми та апарати (стабілізація частоти обертання робочих машин, забезпечення завантажування дробарок тощо).

Об'єкти автоматизації можна класифікувати так:

· прості та складні;

· із зосередженими та розподіленими параметрами.

Рис. 1.5.2. Складний об'єкт – мікроклімат в приміщенні

У простих об'єктів динамічні властивості описуються за допомогою двох узагальнених координат (входу та виходу). Динаміка складних об'єктів для опису потребує не менше трьох координат. Динамічні та статичні властивості об'єктів із зосередженими параметрами постійні в усіх їх просторових точках. Об'єкти із розподіленими, навпаки, потребують ще й просторової координати, оскільки їхня динаміка у різних просторових точках різна. Тому об'єкти із розподіленими координатами є ще й складними.

Властивості об'єкта управління дозволяє визначити алгоритм управління та підібрати комплекс технічних засобів для його реалізації. При цьому користуються математичними моделями об'єктів автоматизації у вигляді передаточних функцій. Передаточні функції (зображення лінійних диференціальних рівнянь) можуть бути одержані за результатами аналітичних та експериментальних досліджень.

Аналітичні методи дослідження об'єктів. У цьому випадку користуються одним із трьох відомих законів збереження: кількості енергії, руху, речовини.

Так, для сільськогосподарського виробництва закони збереження можуть бути інтерпретовані наступним чином:

· для теплових об'єктів

де m – маса об'єкта;

с – питома теплоємність;

θ – температура;

Q_т – сума теплових потоків, що направлені на об'єкт та з нього;

· для об'єктів, що здійснюють круговий рух

де І – момент інерції;

ω – кутова частота обертання;

М – сума моментів;

· для об'єктів, що здійснюють лінійний рух

де V – лінійна швидкість;

F – сума сил, що діють на об'єкт;

· для об'єктів, які наповнюються рідинами

де S – площа основи резервуарів;

h – рівень рідини;

Q – потоки рідин;

• для об'єктів, які піддаються сушінню або зволоженню

де m₀ – маса абсолютно сухої речовини;

ω – відносна вологість;

W – маса вологи, що надходить за одиницю часу.

Аналіз виразів дозволяє записати:

де х, у – вхід та вихід об'єкта;

би – незмінні його властивості.

У кінці ХІХ століття А. Стодола отримав рівняння, яке може бути використане для визначення передаточних функцій об'єктів:

де Т_а – час розгону об'єкту;

δ – коефіцієнт самовирівнювання;

Δх, Δу – відхилення змінних на вході та виході об'єкта.

Залежно від значення коефіцієнта самовирівнювання об'єкти автоматизації поділяються на:

· δ >0 статичні стійкі;

· δ = 0 астатичні;

· δ <0 статичні нестійкі.

Існує також і другий підхід під час побудови математичних моделей об’єктів аналітичним методом – класичний, який потребує знань фізичних явищ, що відбуваються в даному об’єкті.

Аналітичний метод дослідження має одну основну перевагу перед іншими – він значно дешевший (не потребує витрат на експерименти, матеріали), але в той же час моделі за рахунок прийнятих спрощень та допущень не завжди мають достатню точність.

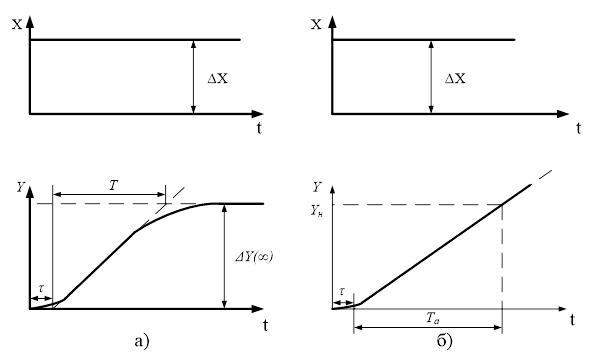
Експериментальні методи досліджень об'єктів поділяються на методи активного та пасивного експерименту. Під час активного експерименту на вхід об'єкта подається сигнал стандартної форми. Реакція об'єкту на цей сигнал дозволяє визначити його передаточну функцію. Найчастіше з усіх випробувальних сигналів використовують прямокутну приступку (рис. 1.5.3).

Рис. 1.5.3. Криві розгону об’єктів:

а – статичних; б – астатичних Т_а

Реакція об'єкта – це крива розгону, яка з метою отримання передаточної функції може оброблятись графічним методом, методом Н. Симою (інтегральних площин) та іншими. Графічна апроксимація полягає в тому, що через точку перегину (для статичного об'єкта) проводять дотичну, яка дозволяє визначити постійну часу Т та час запізнювання τ. Коефіцієнт передачі визначають як . Таким чином, для рис. 1.36,а (статичний об'єкт) передаточна функція матиме структуру:

Для астатичного об'єкта структура передаточної функції має вигляд:

де ε – швидкість розгону об'єкта може бути розрахована як

де у_н – номінальне значення вихідної величини об'єкту управління;

Т_а – час розгону (визначається з рис. 1.36 б).

Необхідно підкреслити, що графічна апроксимація може бути застосованою лише для певного класу об'єктів – тих, у яких точка перегину знаходиться близько до осі абсцис, в іншому випадку точність апроксимації буде невисокою.

Метод інтегральних площин більш універсальний ніж метод графічної апроксимації, дає більшу точність, а тому його можна рекомендувати до використання практично для всіх об'єктів автоматизації.

Структура передаточної функції при цьому має вигляд:

W(р) = W*(р) kе^-ρτ,

де W*(р) – безрозмірна передаточна функція.

Коефіцієнт передачі об'єкта визначається як і за графічної апроксимації. Час запізнювання як час, упродовж якого об'єкт не реагує (або практично не реагує) на вхідний сигнал – прямокутна приступка. Основна робота, як видно, полягає у знаходженні структури та параметрів безрозмірної передаточної функції.

За умов пасивного експерименту об'єкт управління (його вхід та вихід) підключається до вимірювача і упродовж тривалого часу його параметри фіксуються. Використовуючи спеціальні розділи математики (у першу чергу це теорія ймовірності, випадкові процеси), можна розрахувати передаточну функцію об'єкта автоматизації.

Питання для самоконтролю

1. Що може бути об'єктами автоматизації у сільському господарстві? 2. Що дозволяє визначити властивості об'єкта управління? 3. Як записуються закони збереження для теплових об'єктів, для об'єктів, що здійснюють круговий та лінійний рух під час аналітичного методу дослідження об'єктів? 4. Які переваги аналітичного методу дослідження об'єктів автоматизації? 5. У чому полягає графічна апроксимація? 6. Які переваги методу інтегральних площин? 7. Як визначається передаточна функція ?

Попередня тема

На початок

Наступна тема