|
Тіла обертання
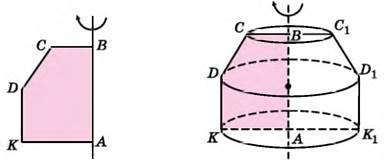 Нехай деякий плоский опуклий
многокутник АBСDК обертається навколо нерухомої прямої, що містить сторону АB. Тоді кожна точка, що належить
многокутнику, крім точок, що належать стороні АB, описує коло, центр якого
належить прямій АB. При цьому весь многокутник АBСDК описує тіло обертання, пряму АB називають віссю цього
тіла обертання. Площина, що проходить через вісь тіла обертання, перетинає
його по деякій фігурі. Цю фігуру називають осьовим перерізом. Осьовим перерізом тіла обертання, зображеного
на малюнку, є многокутник СDКК1D1С1. Нехай деякий плоский опуклий
многокутник АBСDК обертається навколо нерухомої прямої, що містить сторону АB. Тоді кожна точка, що належить
многокутнику, крім точок, що належать стороні АB, описує коло, центр якого
належить прямій АB. При цьому весь многокутник АBСDК описує тіло обертання, пряму АB називають віссю цього
тіла обертання. Площина, що проходить через вісь тіла обертання, перетинає
його по деякій фігурі. Цю фігуру називають осьовим перерізом. Осьовим перерізом тіла обертання, зображеного
на малюнку, є многокутник СDКК1D1С1.
Поверхню, утворену обертанням ламаної BCDKA навколо прямої AB, називають поверхнею
обертання.
Тілом обертання називають таке тіло, яке площинами,
перпендикулярними до деякої прямої (осі обертання), перетинається по кругах
із центрами на цій прямій.
Циліндр та його елементи
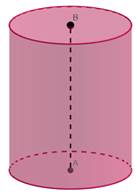 Циліндром називають
геометричне тіло, утворене обертанням прямокутника навколо осі, яка містить
одну з його сторін. Циліндром називають
геометричне тіло, утворене обертанням прямокутника навколо осі, яка містить
одну з його сторін.
Будова циліндра
Переріз циліндра площиною
|
|
|
|
|
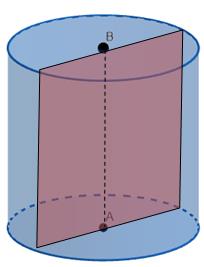
Осьовий переріз, має форму прямокутника – проходить через діагональ основи та містить вісь
циліндра. Якщо осьовим перерізом циліндра є квадрат, то його іноді
називають рівностороннім.
|
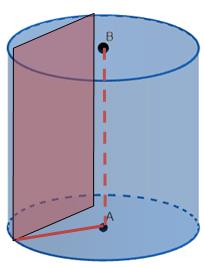
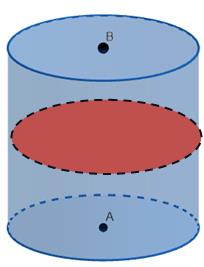
Переріз циліндра, який проходить через хорду основи
на відстані від осі циліндра
|
Переріз циліндра, який проходить паралельно
основам, має форму круга
|
Площа поверхні циліндра
Бічна поверхня циліндра
Якщо поверхню циліндра
розрізати по твірній та по колах основ і розгорнути так, що всі твірні
циліндра будуть належати деякій площині, то отримаємо розгортку бічної
поверхні циліндра.
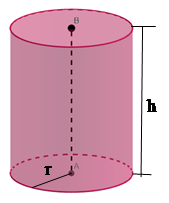

Площа бічної поверхні циліндра Sбічн, радіус основи якого дорівнює r, а висота – h, обчислюється за формулою
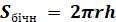 . .
Площа повної поверхні циліндра
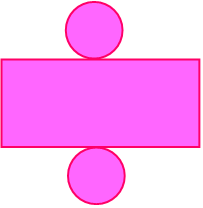 Для того щоб знайти площу повної поверхні циліндра Sповн,
потрібно до площі його бічної
поверхні додати площі двох його основ. Оскільки основою є круг, площа якого
дорівнює Для того щоб знайти площу повної поверхні циліндра Sповн,
потрібно до площі його бічної
поверхні додати площі двох його основ. Оскільки основою є круг, площа якого
дорівнює 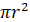 , то маємо , то маємо
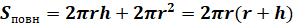
|









