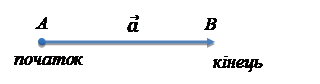|
Прямокутна система координат у просторі
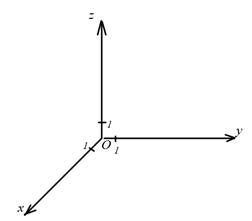 Через довільну точку O простору
проведемо три взаємно перпендикулярні прямі x, y, z. На кожшй з ниx виберемо наїрям, позначивши його стрілкою, та одиничний відрізок. У такий спосіб задають прямокутну
систему кооринат у просторі.
Точку О називають початком координат, а прямі з вибраними
напрямами – осями координат (або координатними
осями). Вісь x називають віссю абсцис, вісь у – віссю ординат, вісь
z – віссю аплікат.
Початок координат розбиває кожну
з осей на дві півосі – додатну (яка містить стрілку напряму) і від'ємну. Через довільну точку O простору
проведемо три взаємно перпендикулярні прямі x, y, z. На кожшй з ниx виберемо наїрям, позначивши його стрілкою, та одиничний відрізок. У такий спосіб задають прямокутну
систему кооринат у просторі.
Точку О називають початком координат, а прямі з вибраними
напрямами – осями координат (або координатними
осями). Вісь x називають віссю абсцис, вісь у – віссю ординат, вісь
z – віссю аплікат.
Початок координат розбиває кожну
з осей на дві півосі – додатну (яка містить стрілку напряму) і від'ємну.
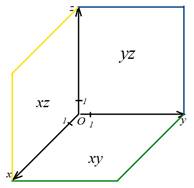
Площини, які проходять відповідно через осі координат x і у, у і z та x і z називають координатними
площинами xy, yz і xz.
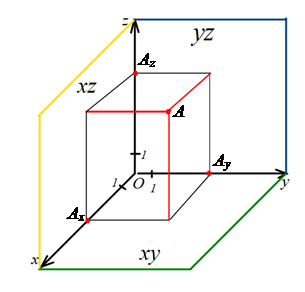 Як
визначити координати
точки Як
визначити координати
точки 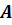 ? ?
1. Щоб
визначити координати
точки 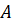 ,
проведемо перпендикуляри з даної точки на координатні площини. ,
проведемо перпендикуляри з даної точки на координатні площини.
2.
З побудованих
основ перпендикулярів, проводимо перпендикуляри на осі системи координат.
3.
Дані
перпендикуляри перетнуть координатні осі в точках 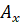 , ,
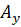 і і 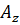 відповідно. Можемо
помітити, що утворивсь прямокутний паралелепіпед, а також, що дані точки можна було отримати
якби будували перпендикулярні площини через
т. відповідно. Можемо
помітити, що утворивсь прямокутний паралелепіпед, а також, що дані точки можна було отримати
якби будували перпендикулярні площини через
т. 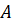 до координатних осей. до координатних осей.
Залежність між
координатами точки та особливістю її розташування
|
Координати точки
|
Особливості розташування точки
|
|
(x; 0; 0)
|
належить осі x
|
|
(0; y; 0)
|
належить осі y
|
|
(0; 0; z)
|
належить осі z
|
|
(x; y; 0)
|
належить площині xy
|
|
(x; 0; z)
|
належить площині xz
|
|
(0; y; z)
|
належить площині yz
|
Формула відстані між
точками 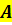 і і 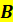 у просторі у просторі
Для знаходження
відстані між двома  і і 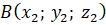 точками у просторі
будемо використовувати формулу: точками у просторі
будемо використовувати формулу:
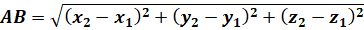
Приклад. Знайдемо відстань між точками 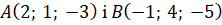
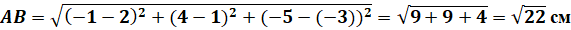
Формула координат
середини відрізка 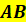 у просторі у просторі
Нехай точка М(xM,
yM, zM) – середина відрідка АВ.
Для знаходження координат середини відрізка у просторі з кінцями в точках  і і 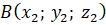 будемо
використовувати формулу: будемо
використовувати формулу:

Приклад. Знайдемо координати середини відрізка між точками 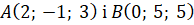
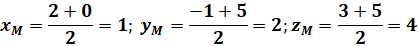
Відповідь. 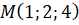
Вектори у просторі
|
Вектор у просторі –
це напрямлений відрізок, тобто відрізок, для якого вказано, яка точка є
його початком, а яка – кінцем.
|
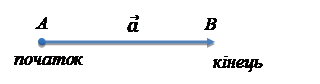
|
|
Позначення вектора:
|
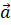 , , 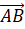
|
|
Модуль (довжина або абсолютна величина) вектора  – це довжина відрізка – це довжина відрізка 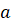 , що зображує вектор , що зображує вектор 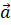 . .
|
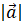
|
|
Нуль-вектор – вектор довжина якого дорівнює нулю (початок і кінець
збігаються в одній точці).
|
|
|
Колінеарні вектори – це два ненульові вектори, що лежать на одній прямій
або паралельних прямих.
|
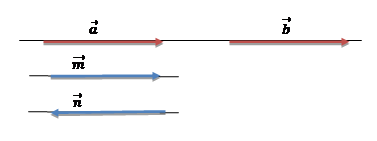
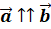 –
співнапрямлені вектори –
співнапрямлені вектори
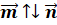 –
протилежнонапрямлені вектори –
протилежнонапрямлені вектори
|
|
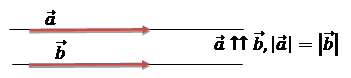
Співнапрямлені вектори з рівними модулями називаються рівними.
|
|
Вектори у просторі
Додавання векторів
|
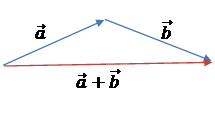
Правило трикутника
|
|
Щоб знaйти суму векторів  і і 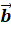 за правилом трикутника, треба: за правилом трикутника, треба:
1) від кіщя вектора 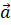 відкласти вектор, що дорівює вектору відкласти вектор, що дорівює вектору 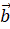 ; ;
2) побудувати вектор, початок якого
збігається з початком вектора 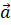 , а кінець – з кінцем вектора , а кінець – з кінцем вектора 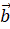 , який і є сумою векторів , який і є сумою векторів 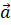 і і 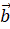 . .
|
|
Правило паралелограма
|

|
Щоб знaйти суму двох
неколінеарних векторів  і і 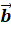 за правилом паралелограма, треба: за правилом паралелограма, треба:
1)
відкласти ці вектори від спільного початку;
2)
побудувати на цих векторах паралелограм;
3) побудувати вектор, що виходить
зі спільної точки і збігається з діагоналлю паралеограма, який і є сумою
векторів 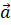 і і 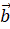 . .
|
|
Правило
паралелепіпеда
|
|
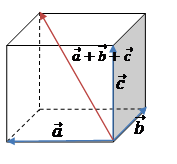
Щоб знйти суму трьох неколінеарних векторів за правилом
паралелепіпеда:
1)
відкладасти дані вектори від спільної точки;
2)
побудувати на даних векторах паралелепіпед;
3)
побудувати діагональ паралелепіпеда, що виходить зі
спільного початку даних векторів, який і буде сумою трьох векторів.
|
Віднімання векторів
|
|
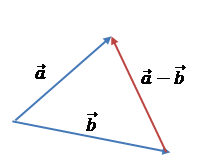
Правило віднімання двох векторів:
1)
Відкласти дані вектори від спільної точки.
2)
Побудувати вектор, початок якого збігається з кінцем
вектора-від’ємника, а кінець – з кінцем вектора-зменшуваного.
3)
Вектор-різниця сполучає кінці векторів 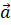 і і 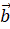 та напрямлений у бік зменшуваного. та напрямлений у бік зменшуваного.
|
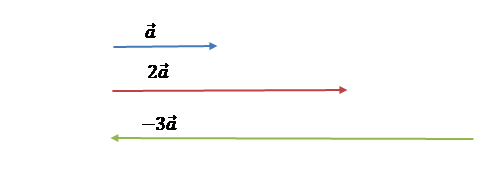
Множення вектора на
число
Властивості множення
вектора на число
Нехай 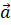 і і 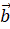 – деякі вектори, – деякі вектори, 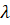 і і 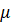 – довільні числа,
тоді маємо рівності: – довільні числа,
тоді маємо рівності:
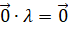 ; ;
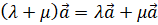 ; ;
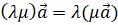 ; ;

Вектор 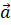 , колінеарний вектору , колінеарний вектору 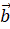 , можна подати у вигляді , можна подати у вигляді 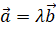 , , 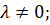 і навпаки, якщо і навпаки, якщо
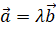 , де , де 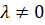 , то вектори , то вектори 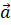 і і 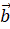 – колінеарні. – колінеарні.
|