|
Паралельне проєктування, його властивості
 Паралельне
проєктування – це
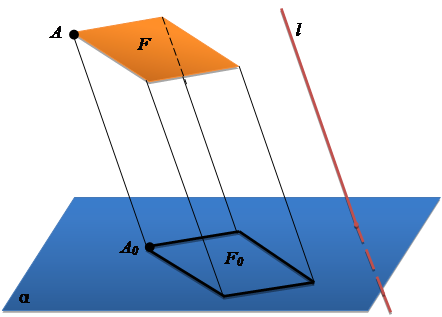
зображення довільної геометричної фігури на площині, при якому всі точки фігури переносяться на площину по прямих, паралельних заданій, яка називається напрямом проєктування. Паралельне
проєктування – це
зображення довільної геометричної фігури на площині, при якому всі точки фігури переносяться на площину по прямих, паралельних заданій, яка називається напрямом проєктування.
Наприклад,
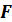 – оригінал
фігури; – оригінал
фігури;
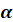 – площина
проєкції; – площина
проєкції;
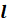 – проєктуюча пряма; – проєктуюча пряма;
Через довільну
точку 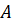 фігури фігури 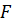 проведемо
пряму, паралельну проєктуючій прямій проведемо
пряму, паралельну проєктуючій прямій 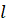 . Ця пряма перетне площину . Ця пряма перетне площину 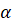 в точці в точці 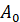 , тоді: , тоді:
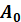 – зображення
т. – зображення
т. 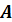 в площині в площині 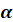 . .
Побудувавши в такий спосіб всі точки фігури 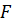 отримаємо в
площині отримаємо в
площині 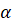 фігуру фігуру 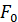 . .
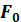 – паралельна проєкція фігури – паралельна проєкція фігури 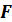 на площину на площину 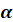 . .
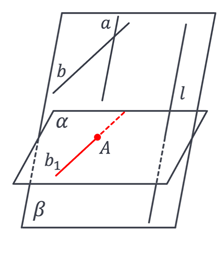
Розглянемо можливі паралельні проєкції прямих  , які перетинаються. , які перетинаються.
|
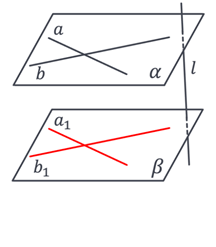
Якщо проєктуюча пряма не лежить в одній площині з даними прямими і не паралельна жодній даній прямій, то отримаємо дві прямі.
|
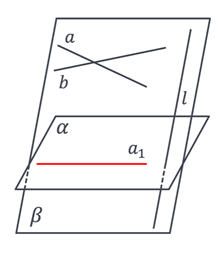
Якщо проєктуюча пряма лежить в одній площині з даними прямими і не паралельна жодній даній прямій, то отримаємо пряму.
|
Якщо проєктуюча пряма лежить в одній площині з даними прямими і паралельна одній з даних прямих, то отримаємо пряму і точку.
|
|
|
|
|
|
Дві прямі, що перетинаються
|
Пряма
|
Пряма і
точка
|
Властивості паралельного проєктування
|
|
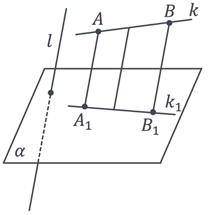
Проєкцією прямої є пряма.
Проєкцією відрізка є відрізок.
|
|
|
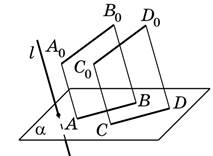
Проєкції паралельних прямих
паралельні між собою або збігаються.
Проєкції двох паралельних
відрізків лежать на паралельних
прямих або на одній прямій.
|
|
|
|
|
|
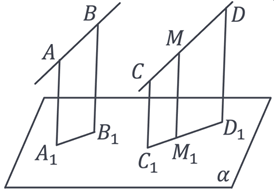
Якщо відрізки лежать на одній
або паралельних прямих, то відношення їх проєкцій дорівнює відношенню самих відрізків.
Наприклад:
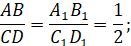
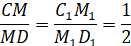
|
|
Наслідок:
Середина відрізка проєктується в середину
його проєкції.
|
|
|
|
Зображення фігур у стереометрії
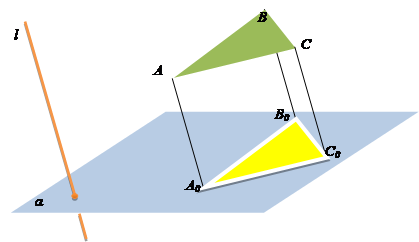
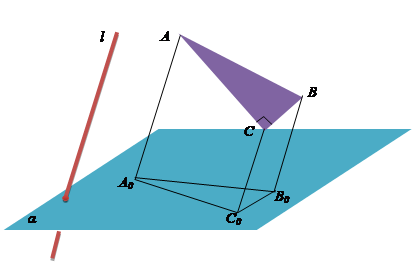
Ø Проєкцією кожного трикутника
може бути трикутник довільного
виду.
Ø Проєкцією мeдіaни трикутника є мeдіaнa проєкці трикутника, а проєкцією
середньої лінії трикутника – є середня
лінія проєкції трикутника.
|
|
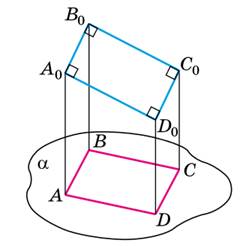
ØПроєкцією кожного пapaлeлoгpaмa є пapaлeлoгpaм дoвільнoгo виду
(Дoвільний пapaлeлoгpaм
може бути проєкцією прямокутника, ромба, квадрата).
|
|
|
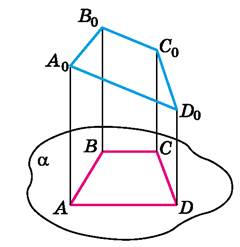
ØОскільки проєкцією паралельниx
відрізків є паралельні відрізки, то проєкцією трапеції є трапеція. Якщо ABCD – проєкція трапеції A0B0C0D0 з основами A0D0 і B0C0, то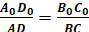 або або 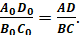
|
|
|
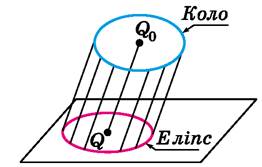
Ø
Пapaлeльнy проєкцію кола нaзивaють еліпсом. Точку Q, яка є проєкцією
центра кола – точки Q0, називають
центром еліпса.
|
|












