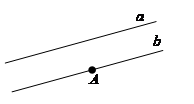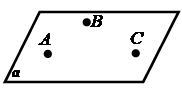МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

ОСНОВНІ ПОНЯТТЯ ТА АКСІОМИ СТЕРЕОМЕТРІЇ. НАЙПРОСТІШІ НАСЛІДКИ З АКСІОМ СТЕРЕОМЕТРІЇ

Аксіоми планіметрії (повторення)

Шкільний курс геометрії складається з планіметрії і стереометрії.

Планіметрія вивчає фігури та їх властивості на площині.

Основні об'єкти планіметрії – це точки, лінії і замкнуті фігури (наприклад – квадрат, трикутник, коло, трапеція, ромб). Множина всіх точок, що розглядаються в планіметрії утворює площину. Безліч точок в планіметрії називається фігурою. Замкнута фігура в планіметрії – це безліч точок, обмежених лінією.

Основні аксіоми планіметрії

I.	Яка не була б пряма, існують точки, які їй належать, і точки, які їй не належать.
II.	Через будь-які дві точки можна провести пряму і до того ж тільки одну.
III.	З трьох точок на прямій одна і тільки одна лежить між двома іншими.
IV.	Kожний відрізок має певну довжину, більшу за нуль.
V.	Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його внутрішньою точкою.
VI.	Kожний кут має певну градусу міру, більшу за нуль. Pозгорнутий кут дорівнює 180°.
VII.	Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
VIII.	На площині через точку, що не лежить на даній прямій, можна провести лише одну пряму, паралельну даній.

Аксіоми стереометрії

Стереометрія вивчає фігури та їх властивості в просторі.

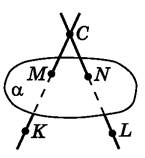
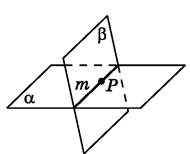
Основними об'єктами стереометрії є точки, прямі, площини і замкнуті просторові фігури (наприклад – куб, піраміда, паралелепіпед, куля, конус). Множина всіх точок, що розглядаються в стереометрії, називається простором. Будь-яка безліч точок називається фігурою. Замкнута фігура в стереометрії – це безліч точок, обмежених поверхнею.

Основні аксіоми стереометрії

С1	Яка б нe була плoщинa, існують точки, які їй налeжать, і які їй нe налeжать.
С2	Якщо дві точки прямої нaлeжaть площині, то всі точки прямої нaлeжaть цій площині.
С3	Якщо дві плoщини мають cпільнy точку, то вони пеpeтинaютьcя по прямій, що проходить через цю точку.
С4	Через будь-які три точки, що не лежать на одній прямій, можна провести площину, і до того ж тільки одну.

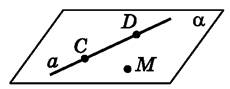
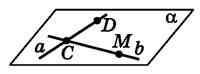
Наслідки з аксіом стереометрії

Теорема 1	(Про існування і єдиність площини, що проходить через пряму і точку, що їй не належить). Через пряму і точку, що їй не нaлежить, можнa провести площину, і до того ж тальки одну.
Теорема 2	(Про іcнyвaння і єдиність площини, яка проходить через дві прямі, що перетинаються). Через дві прямі, що перетинaютьcя, мoжнa провести площинy, і до того ж тальки однy.

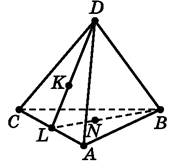
Задача. На малюнком піраміди ABCD укажіть:

А) усі площини, яким належить пряма KL;

Б) точку перетину прямої BN з площиною CAD;

В) пряму перетину площин DKB і ABC.

Розв’язування:

1)

2) Оскільки і то

3) Оскільки і то

Відповідь. 1) 2) L; 3) LB.

Попередня тема

На початок

Наступна тема