|
Обернені тригонометричні
функції
Арксинусом числа b, де 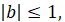 називають
таке число α із проміжку називають
таке число α із проміжку 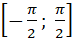 , синус
якого дорівнює b ( , синус
якого дорівнює b (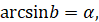 якщо якщо 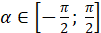 і і 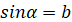 ). ).
Наприклад,
якщо 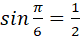 ,
то ,
то 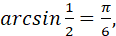 оскільки оскільки 
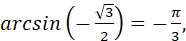 бо бо 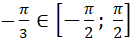 і і 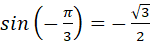 ; ;
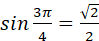 , але , але 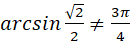 , оскільки , оскільки 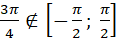 . .
Арккосинусом числа b, де 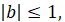 називають
таке число α із проміжку називають
таке число α із проміжку 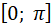 , косинус якого дорівнює b
( , косинус якого дорівнює b
(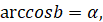 якщо якщо 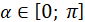 і і 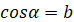 ). ).
Наприклад,
якщо 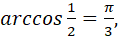 оскільки оскільки 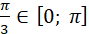 і і 
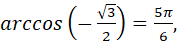 бо бо 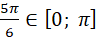 і і 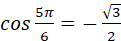 ; ;
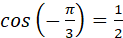 , але , але 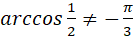 , оскільки , оскільки 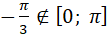 . .
Арктангенсом числа b  називають
таке число α із проміжку називають
таке число α із проміжку 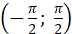 , тангенс якого дорівнює b
( , тангенс якого дорівнює b
(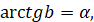 якщо якщо 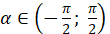 і і 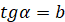 ). ).
Наприклад,
якщо 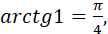 оскільки оскільки  і і 
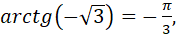 бо бо 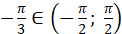 і і 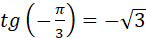 ; ;
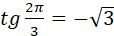 , але , але 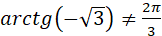 , оскільки , оскільки 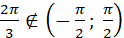 . .
Арккотангенсом числа b  називають
таке число α із проміжку називають
таке число α із проміжку 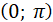 , котангенс якого дорівнює b
( , котангенс якого дорівнює b
(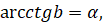 якщо якщо 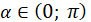 і і 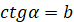 ). ).
Наприклад,
якщо 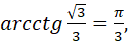 оскільки оскільки 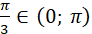 і і 
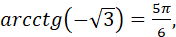 бо бо 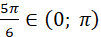 і c і c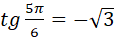 ; ;
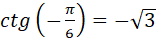 , але , але 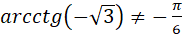 , оскільки , оскільки 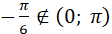 . .
Враховуючи парніть та непарність обернених тригонометричних функцій, маємо наступні рівності:
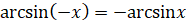 (функція arcsin непарна) (функція arcsin непарна)
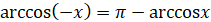 (функція arccos ніпарна, ні непарна) (функція arccos ніпарна, ні непарна)
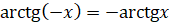 (функція arctg непарна) (функція arctg непарна)
 (функція arcctg ні парна, ні непарна) (функція arcctg ні парна, ні непарна)
Найпростіші тригонометричні
рівняння
Þ
Рівняння 
|
Рівняння 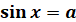 , де a – деяке число , де a – деяке число
|
|
a < –1 або a > 1
|
Розв’язків немає
|
|
ЧАСТКОВІ ВИПАДКИ
|
a=1
|


|

|
|
|
a=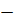 1 1
|

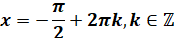
|
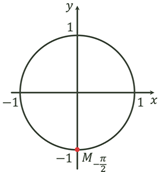
|
|
|
a=0
|
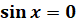

|

|
|
|
|
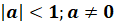
|

|
|
Þ Рівняння 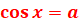
|
Рівняння 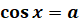 , де a – деяке число , де a – деяке число
|
|
a <
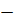 1
або a > 1 1
або a > 1
|
Розв’язків немає
|
|
ЧАСТКОВІ ВИПАДКИ
|
a=1
|


|

|
|
a=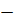 1 1
|


|

|
|
a=0
|
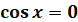

|

|
|
|
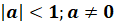
|

|
Þ
Рівняння 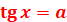 і і 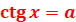
|
|





