МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ

Елементи математичної статистики

Статистикою називають науку, яка збирає, обробляє і вивчає різні дані, пов’язані з масовими явищами, процесами та подіями.

Усю сукупність, з якої роблять вибір одиниць спостереження, називають генеральною. Наприклад, зі 100 деталей для спостереження вибирають 10. 100 деталей – генеральна сукупність.

Сукупність одиниць, дібраних для вибіркового спостереження, називають вибіркою. Для того щоб за вибіркою можна було судити про властивості генеральної сукупності, вибірка має бути представницькою (репрезентативною).

Якщо у вибірці присутні всі значення випадкової величини в тих самих пропорціях, що й у генеральній сукупності, то цю вибірку називають репрезентативною. Наприклад, потрібно утворити вибірку з генеральної сукупності великого обсягу, якою є виготовлені заводом трактори. Кожному трактору присвоюють номер, який заносять до таблиці. Якщо у вибірці має бути 30 тракторів, то з таблиці навмання вибирають 30 чисел і трактори з відповідними номерами підпадають під проведення контролю. Після того як вибірка утворена, і її об’єкти обстежують щодо властивості, яку досліджують, і в результаті отримують дані, які досліджують. Оскільки номери у таблиці (а значить і відповідні трактори) вибрані випадково, то репрезентативність вибірки буде забезпеченою.

Обробка результатів спостережень, яка полягає, наприклад, у тому, що отримані наслідки спостережень розташовують у порядку неспадання, називають ранжуванням дослідних даних, а одержаний при цьому ряд чисел називають ранжированим рядом. Наприклад, відділ технічного контролю заводу виміряв глибину пазів у 20 однотипних деталях. Одержали такий результат (у см): 2,1; 3; 1; 1; 2; 3; 1; 1; 2,2; 3; 1; 2,1; 3,2; 2,2; 3; 2,3; 1; 2; 2; 3,3. Такий ряд не дозволяє судити про закономірності, закладені в розподілених даних. Розташуємо дані ряду в порядку неспадання. Одержимо ранжирований ряд: 1; 1; 1; 1; 1; 1; 2; 2; 2; 2,1; 2,1; 2,2; 2,2; 2,3; 3; 3; 3; 3; 3,2; 3,3. Можемо зробити висновок, що 6 деталей мають глибину пазу 1 см, 3 деталі – 2 см, 2 деталі – 2,1 см і т. д. Тепер легше встановити: навколо якої величини групується більшість показників; які є відхилення від цієї величини; яка загальна картина розподілу.

Числове значення кількісної ознаки заданого члена статистичної сукупності називають варіантою. Позначають: , де і – індекс варіанти. Варіантами у наведеному вище прикладі є: 1; 2; 2,1; 2,2; 2,3; 3; 3,2; 3,3.

Частота – це число, яке показує, скільки разів трапляється кожна варіанта. Позначають де i – індекс варіанти. Загальна сума частот дорівнює: . Частотами у наведеному вище прикладі є:

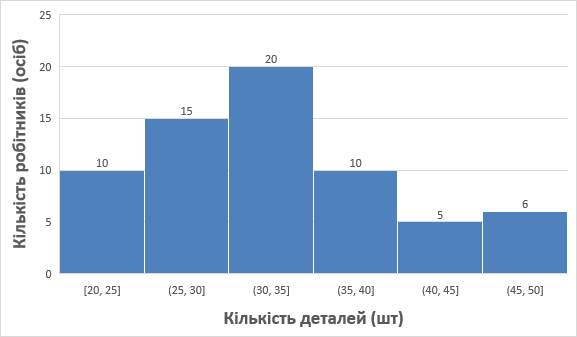
Гістограма частот – це фігура, що складається з прямокутників, які спираються на інтервали угруповання.

Кількість деталей (шт)	Кількість робітників (осіб)
20–25	10
25–30	15
30–35	20
35–40	10
40–45	5
45–50	6
Загальна кількість	66

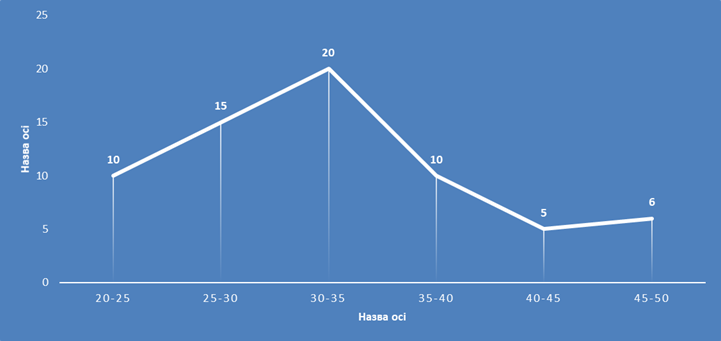
Полігон частот – один зі способів графічного зображення густини ймовірності випадкової величини. Полігон є ламаною, що сполучає точки, які відповідають серединним значенням інтервалів угруповання і частотам цих інтервалів.

При оцінюванні даних за розподілом частот використовують моду, медіану та середні значення.

Модою називають значення ознаки варіанти, яке трапляється найчастіше в даному ряді розподілу. Позначають: . Наприклад, за результатами написання контрольної роботи учні отримали такі бали: 5 балів – 2 учні; 6 балів – 3 учні; 7 балів – 8 учнів; 8 балів – 10 учнів; 9 балів – 2 учні; 10 балів – 4 учні; 11 балів – 3 учні; 12 балів – 2 учні. Модальним номером є 8 балів, оскільки він має найбільшу чисельність – 10 учнів. Отже, .

У групі значень 2; 4; 4; 4; 5; 7; 7; 10; 10; 10 модами є .

Медіаною вибірки називають число, яке поділяє навпіл упорядковану (у порядку зростання чи спадання ознаки) сукупність усіх значень вибірки. Позначають .

Наприклад, медіана групи значень 5, 7, 11, 13, 19 буде 11. .

Медіана групи значень 3, 4, 8, 16, 17, 19 дорівнює 12:

Середнім значенням (середнім арифметичним) називають таке число , яке отримують діленням суми всіх даних вибірки на кількість цих даних п:

Середнє геометричне _с для додатних чисел визначають за формулою .

Приклад. На діаграмі відображено нараховану фірмою загальну суму заробітної плати усім своїм працівникам у січні, лютому та березні 2011 року. У січні на фірмі працювали 15 співробітників, у лютому – 18, а в березні – 25. Як змінилася середня нарахована заробітна плата в цій фірмі в березні порівняно з січнем?

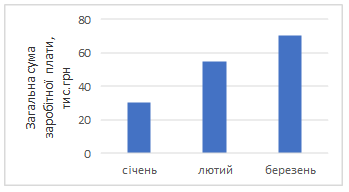
Розв'язання.

Середня заробітна плата в січні

Середня заробітна плата в березні

Отже, на 800 грн. Збільшилася заробітна плата у березні порівняно з січнем.

Попередня тема

На початок