МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

ЕЛЕМЕНТИ КОМБІНАТОРИКИ. КОМБІНАТОРНІ ПРАВИЛА СУМИ ТА ДОБУТКУ

Елементи теорії множин

Поняття множини належить до основних понять математики.

Множину вважають заданою, якщо вказано властивість, яку мають усі її елементи і не мають жодні інші об’єкти. Наприклад, множина учнів класу, множина дерев у саду, множина парних чисел.

Кожний об’єкт, який входить до множини, називають елементом цієї множини. Множину, яка ні містить жодного елемента, називають порожньою множиною.

Множини позначають великими буквами латинського алфавіту, а їхні елементи – малими літерами латинського алфавіту. Порожню множину позначають символом «». Запис означає, ще елемент а належить множині А, а запис означає, що елемент b не належить множині А.

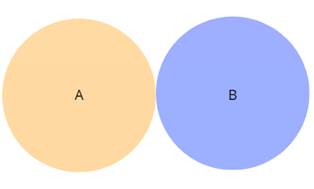
Множини бувають скінченні та нескінченні. Наприклад, множина літер українського алфавіту скінченна. Для скінченної множини А через m(А) позначають число її елементів. Число елементів порожньої множини дорівнює 0. Множина натуральних чисел, множина простих чисел, множина точок прямої – нескінченні множини.

Якщо кожний елемент множини А є елементом множини В, то множину А називають підмножиною множини В. Позначають: . Кожна множина є підмножиною сама собі:
. Порожня множина є підмножиною будь-якої множини: .

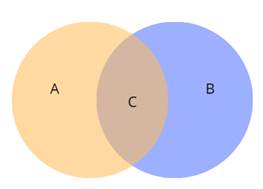
Дві множини називають рівними, якщо вони складаються з однакових елементів. Наприклад, А – множина коренів рівняння , В – множина коренів рівняння . Тоді і }. Отже, множини А та В рівні (А = В).

Перерізом (добутком) множин А та В називають множину С, яка складається з усіх тих і лише тих елементів, які належать кожній з даних множин. Позначають:. Якщо , то i і навпаки, якщо і , то .

Якщо множини А та В не мають спільних елементів, то перерізом цих множин є порожня множина: .

Об’єднанням (сумою) множин А та В називають множину С, яка складається з усіх тих і лише тих елементів, які належать хоча б одній із множин А або В. Позначають: . Якщо , то або і навпаки, якщо або , то .

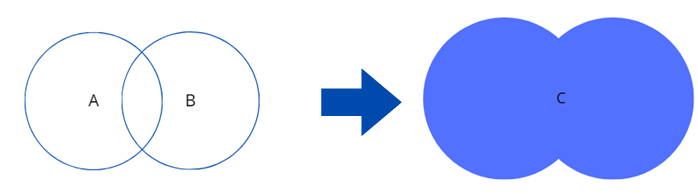
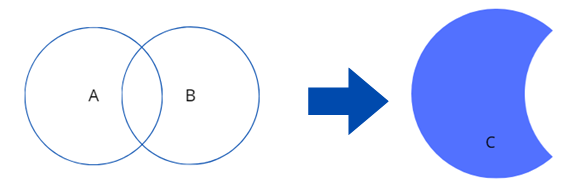
Наприклад, об’єднанням множин гострокутних, тупокутних і прямокутних трикутників є множина всіх трикутників.

Різницею двох множин А та В називають таку множину С, яка складається лише з усіх тих едемі нтів множини А, які не належать множині В. Позначають: або .

Якщо множини А та В такі, що , то множину С, яка містить лише усі елементи множини А, які не належать множині В, називають доповненням множини В до множини А.

Елементи комбінаторики

Комбінаторика – розділ математики, у якому вивчають способи вибору та розташування елементів з деякої скінченної множини, які відповідають певним умовам. Вибрані (або вибрані та розташовані) групи елементів називають сполуками. Комбінаторика вивчає такі сполуки: розміщення, перестановки, комбінації (сполучення) тощо.

Комбінаторні правила суми та добутку

Комбінаторне правило суми: якщо деякий об’єкт А можна вибрати m способами, а елемент В – k способами (причому будь-який вибір елемента А відрізняється від вибору елемента В), то вибрати А або В можна m+k способами.

Приклад. Є 5 різних олівців і 7 різних ручок. Скількома способами можна обрати один елемент: одну ручку або однин олівець?

Розв’язання. Оскільки портібно обрати лише один елемент, застосуємо правило суми:

Правило суми можна поширити на три й більше елементів.

Комбінаторне правило добутку: якщо деякий елемент А можна вибрати m способам, а після кожного такого вибору інший елемент В можна вибрати (незалежно від вибору елемента A) k способами, то пару об’єктів А і В можна вибрати способами.

Приклад. Є 5 різних олівців і 7 різних ручок. Скількома способами можна утворити набір з однієї ручки й одного олівця?

Розв’язання. Оскільки маємо обрати пару елементв, то застосуємо правило добутку

Попередня тема

На початок

Наступна тема