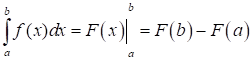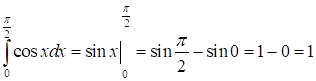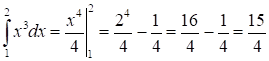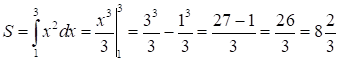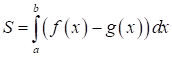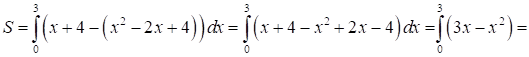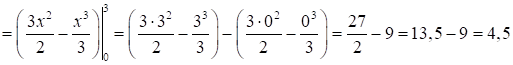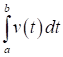МАТЕМАТИКА

(АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ ТА ГЕОМЕТРІЯ)

Електронний посібник

ГОЛОВНА	ЗМІСТ	АНОТАЦІЯ	ДОДАТКИ
НАВЧАЛЬНА ПРОГРАМА		СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ	УКЛАДАЧІ

ІНТЕГРАЛ, ЙОГО ФІЗИЧНИЙ ТА ГЕОМЕТРИЧНИЙ ЗМІСТ

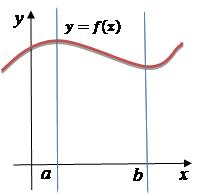
Визначений інтеграл

Теорема (про площу криволінійної трапеції). Нехай – функція неперервна на проміжку , яка на цьому проміжку набуває лише невід’ємних значень, а – первісна цієї функції на цьому проміжку. Тоді площу криволінійної трапеції, обмеженої графіком функції , віссю абсцис і прямими і , обчислюють за формулою: Різницю називають визначеним інтегралом функції на проміжку і позначають .

Тоді маємо: . Дану формулу називають формулою Ньютона-Лейбніца.

Приклад. Обчисліть інтеграл

Розв’язання.

Приклад. Обчисліть інтеграл .

Розв’язання.

Фізичний та геометричний зміст визначеного інтегралу

Геометричний зміст визначеного інтеграла:

Інтеграл від функції , яка неперервна на проміжку і набуває на цьому проміжку лише невід’ємних значень, є площею криволінійної трапеції, обмеженої графіком цієї функції та прямими .

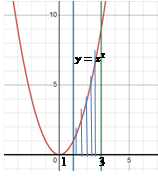
Приклад. Обчисліть площу криволінійної трапеції, обмеженої графіком функції і прямими

Розв’язання.

Якщо фігура обмежена зверху графіком функції а знизу – графіком функції та вертикальними прямими і , причому функції і неперервні на проміжку і для всіх значень справджується нерівність , тоді площу такої фігури можна обчислити за формулою

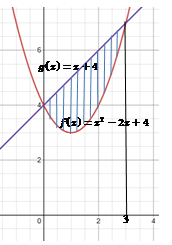
Приклад. Знайти площу фігури, обмежену функціями і

Розв’язання.

Знайдемо точки перетину графіків функцій: Оскільки , то площа фігури дорівнює:

Фізичний зміст визначеного інтеграла:

Інтеграл є переміщенням за інтервал часу матеріальної точки, що рухається прямолінійно зі швидкістю .

Приклад. Матеріальна точка рухається прямолінійно зі швидкістю (м/с). Знайдіть
(у м) переміщення точки за проміжок часу від до

Розв’язання.

Приклад. Тіло рухається прямолінійно зі швидкістю Знайти закон руху тіла якщо

Розв’язання.

Закон руху знайдемо як загальний вигляд первісної

За умовою , тоді .

Отже,

Попередня тема

На початок

Наступна тема