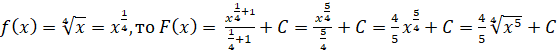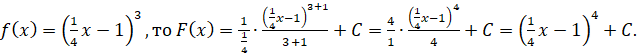|
Первісна та її властивості
Функцію 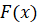 називають первісною для функції називають первісною для функції
 на заданому проміжку,
якщо для всіх х із цього проміжку на заданому проміжку,
якщо для всіх х із цього проміжку
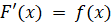 . .
Знаходження функції  за її
похідною називають операцією інтегрування
(від лат. integratio – відновлення). Ця операція є оберненою до операції диференціювання. за її
похідною називають операцією інтегрування
(від лат. integratio – відновлення). Ця операція є оберненою до операції диференціювання.
Наприклад
Для функції f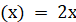 на
проміжку на
проміжку 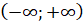 первісною
є функція первісною
є функція 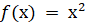 , оскільки для кожного , оскільки для кожного 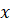 із цього
проміжку виконується рівність із цього
проміжку виконується рівність 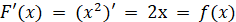 . .
Зауважимо, що, наприклад, функція 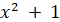 має ту
саму похідну, що й функція має ту
саму похідну, що й функція 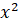 , дійсно , дійсно 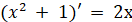 . Тому функція . Тому функція 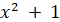 є також
первісною для функції є також
первісною для функції 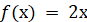 . Зрозуміло, що замість числа 1 можна підставити
будь-яке інше число С, матимемо . Зрозуміло, що замість числа 1 можна підставити
будь-яке інше число С, матимемо 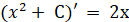 . Звідси приходимо до висновку: задача знаходження первісної має безліч розв’язків
у тому випадку, коли хоча
б один з розв’язків можна
знайти. . Звідси приходимо до висновку: задача знаходження первісної має безліч розв’язків
у тому випадку, коли хоча
б один з розв’язків можна
знайти.
Теорема (основна властивість первісної). Кожна з первісних для функції
 на
заданому проміжку має вигляд на
заданому проміжку має вигляд 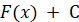 , де , де 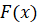 – одна із
цих первісних, а – одна із
цих первісних, а 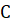 – довільна стала. – довільна стала.
Приклад, Оскільки для функції 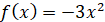 на проміжку на проміжку 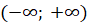 однією з
первісних є функція – однією з
первісних є функція –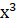 (дійсно (дійсно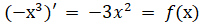 ), то загальний вигляд усіх первісних для функції ), то загальний вигляд усіх первісних для функції
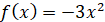 можна
записати у вигляді можна
записати у вигляді 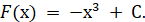
Невизначений інтеграл
Сукупність усіх первісних для функції  називають невизначеним інтегралом
і позначають символом називають невизначеним інтегралом
і позначають символом 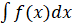 . .
Тут 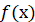 – підінтегральна
функція, х - змінна інтегрування. – підінтегральна
функція, х - змінна інтегрування.
Таким чином: 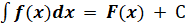 , ,
де F(х) – одна з первісних, а С
– довільна стала.
Приклад, Оскільки 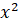 – первісна для – первісна для 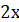 , то , то 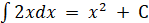 . .
Таблиця первісних
|
Фуккція 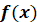
|
Загальний викляд первісних 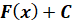
|
|
0
|
C
|
|
1
|
x+C
|
|
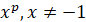 , p – число , p – число
|
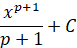
|
|

|
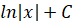
|
|

|
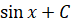
|
|
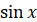
|
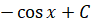
|
|
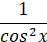
|

|
|
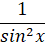
|
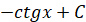
|
|
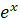
|
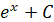
|
|
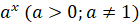
|
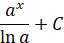
|
Приклад. Знайти первісні елементарних функцій:
1) 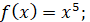 2) 2) 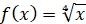 ; 3) ; 3) 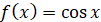 ; 4) ; 4) 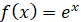 . .
Розв’язання.
R
якщо 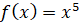 , то , то 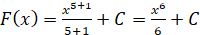 ; ;
R
якщо 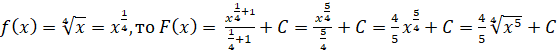 ; ;
R
якщо 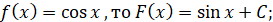
R
якщо 
Приклад. Для функції 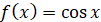 знайдіть первісну, графік якої проходить
через точку знайдіть первісну, графік якої проходить
через точку 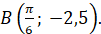
Розв’язання/
Загальний вигляд первісної для функції 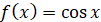 є функція є функція 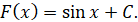 За умовою графік первісної
функції проходить через точку За умовою графік первісної
функції проходить через точку 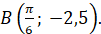 Тому маємо рівність: Тому маємо рівність:
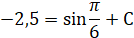
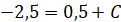
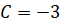
Отже, шукана первісна 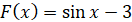
Правила знаходження
первісних
Правило 1. Якщо 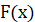 – первісна для – первісна для 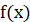 , а , а 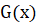 – первісна для – первісна для 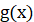 , то , то 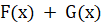 – первісна для – первісна для 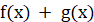 . .
Приклад. Знайти первісну для функції 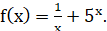
Розв'язання.
Якщо 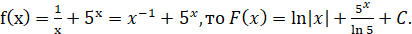
Правило 2. Якщо 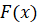 – первісна для – первісна для  , а , а 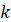 – стала, то – стала, то 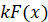 – первісна для – первісна для 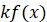 . .
Приклад. Знайти первісну для функції 
Розв’язання.
Якщо 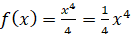 , то , то 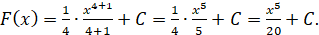
Правило 3. Якщо 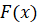 – первісна для – первісна для  , а , а 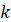 і і 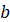 – деякі сталі, причому – деякі сталі, причому 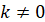 , ,
тоді 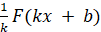 – первісна – первісна 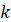 для
функції для
функції 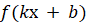 . .
Приклад. Знайти первісну для функції 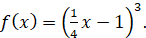
Розв’язання.
Якщо 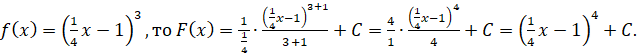
|