|
Логарифмічні рівняння
Рівняння називають логарифмічним, якщо воно містить змінну лише під
знаком логарифма.
Способи розв’язування логарифмічних рівнянь
Рівняння виду 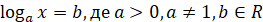 , розв’язується
використовуючи означення логарифму. Тоді, , розв’язується
використовуючи означення логарифму. Тоді, 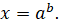
Рівняння виду 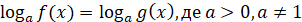 , рівносильне системі , рівносильне системі
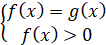 або або 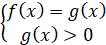
|
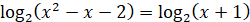
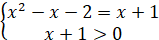
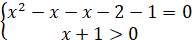
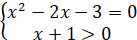
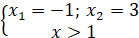
Отже, 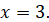
|
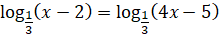
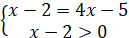
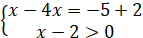
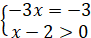
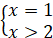
Отже, рівняння розв’язку не має.
|
|
Рівняння виду 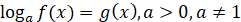 , рівносильне рівнянню , рівносильне рівнянню

|
|
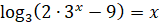
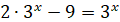
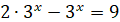
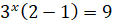
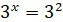
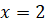
|

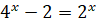
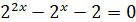
Заміна 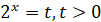
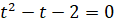
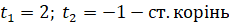
Повернення до заміни
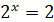
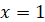
|
|
Використання властивостей логарифмів
(із врахуванням області допустимих значень)
|
|
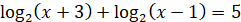
ОДЗ: 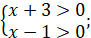 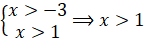
Використаємо формулу суми логарифмів

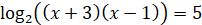
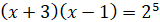
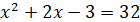
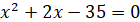
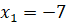 - не задовільняє ОДЗ - не задовільняє ОДЗ
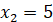
Отже, 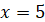
|
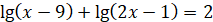
ОДЗ: 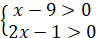 ; ; 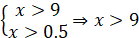
Використаємо формулу суми логарифмів

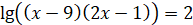
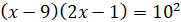
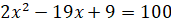
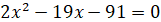
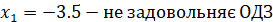
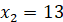
Отже, 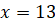
|
|
Використання заміни 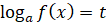
|
|
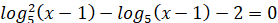
ОДЗ: 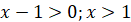
Заміна 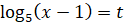
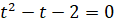
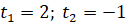
Повернення до заміни
1)
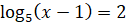 ; ; 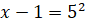 ; ;
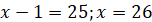
2)
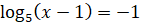 ; ;
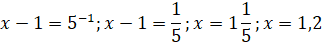
Отже, 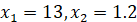
|
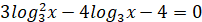
ОДЗ: 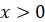
Заміна 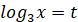
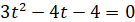
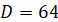
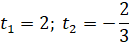
Повернення до заміни:
1)
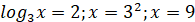
2)
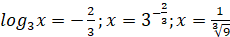
|
Логарифмічні нерівності
Нерівність називають логарифмічним, якщо вона містить змінну лише під знаком логарифма (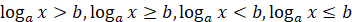 ). ).
Правила розв’язання нерівностей:
R Якщо 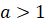 , то при переході до нерівності-наслідку знак
нерівності залишаємо без змін, якщо , то при переході до нерівності-наслідку знак
нерівності залишаємо без змін, якщо 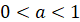 – знак
нерівності змінюється на протилежний. – знак
нерівності змінюється на протилежний.
R Якщо
в отриманій нерівності-наслідку
сплавджується нерівність:
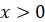 (ОДЗ), то отриману
нерівність жодною додатковою умовою не доповнюємо; якщо ж не виконується, то доповнюємо таку нерівність умовою (ОДЗ), то отриману
нерівність жодною додатковою умовою не доповнюємо; якщо ж не виконується, то доповнюємо таку нерівність умовою 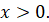
Способи розв’язування логарифмічних нерівностей
|
Нерівності виду 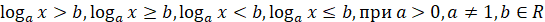
|
|
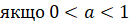 , то , то 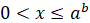
|
якщо 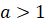 , то , то 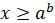
|
|
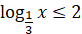
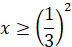
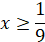
|
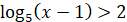
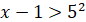
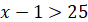
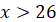
|
|
Нерівність виду 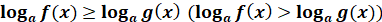
|
|
При 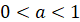

|
При 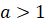
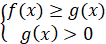
|
|
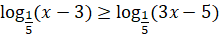
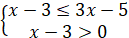
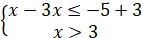
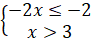
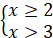
Отже, 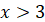
|
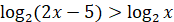
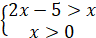
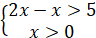
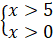
Отже, 
|
|
Використання властивостей логарифмів
|
|
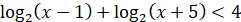
ОДЗ: 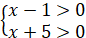 ; ; 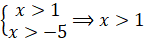
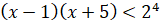
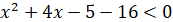
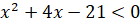
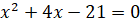
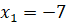 , , 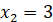
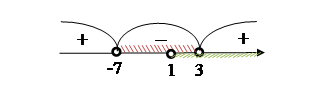
Отже, 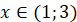
|
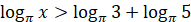
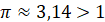
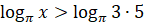
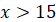
|
|
